people have died from curable diseases

since this page started loading...

💀

dFDA: A Decentralized Framework for Drug Assessment Using Two-Stage Real-World Evidence Validation

We present the Predictor Impact Score (PIS), a novel composite metric operationalizing Bradford Hill causality criteria for automated signal detection from aggregated N-of-1 observational studies. Combined with pragmatic trial confirmation following the RECOVERY model, this two-stage framework generates validated outcome labels at ~80x lower cost than traditional Phase III trials. This enables continuous, population-scale pharmacovigilance and precision dosing recommendations.

Author

Affiliation

Mike P. Sinn

Decentralized Institutes of Health

Doi

10.5281/zenodo.18203376

Keywords

pharmacovigilance, real-world evidence, N-of-1 trials, causal inference, Bradford Hill criteria, treatment effects, adverse events, outcome labels, variable relationships, predictor-outcome analysis

1 Abstract

Current pharmacovigilance systems rely primarily on spontaneous adverse event reporting, which suffers from significant underreporting, lack of denominator data, and inability to quantify effect sizes. Meanwhile, the proliferation of wearable devices, health apps, and patient-reported outcomes has generated unprecedented volumes of longitudinal real-world data (RWD) that remain largely untapped for safety and efficacy signal detection.

We present a comprehensive two-stage framework for generating validated outcome labels with quantitative effect sizes:

Stage 1 (Signal Detection): Aggregated N-of-1 observational analysis^8,9 integrates data from millions of individual longitudinal natural experiments. The methodology applies temporal precedence analysis with automated hyperparameter optimization, addresses six of nine Bradford Hill causality criteria through a composite Predictor Impact Score (PIS), and produces ranked treatment-outcome hypotheses at ~$0.100 (95% CI: $0.030-$1.00) per patient.

Stage 2 (Causal Confirmation): High-priority signals (top 0.1-1% by PIS) proceed to pragmatic randomized trials following the RECOVERY/ADAPTABLE model^10,11. Simple randomization embedded in routine care confirms causation at ~$500 (95% CI: $400-$2.50K) per patient (82x (95% CI: 50x-94.1x) cheaper than traditional Phase III trials) while eliminating confounding concerns inherent in observational data.

The complete methodology includes: (1) data collection from heterogeneous sources; (2) temporal alignment with onset delay optimization; (3) within-subject baseline/follow-up comparison; (4) Predictor Impact Score calculation operationalizing Bradford Hill criteria; (5) Trial Priority Score for signal-to-trial prioritization; (6) pragmatic trial protocols for causal confirmation; and (7) validated outcome label generation with evidence grades.

This two-stage design addresses the fundamental limitations of purely observational pharmacovigilance (confounding, self-selection, and inability to prove causation) while maintaining the scale and cost advantages of real-world data. The result is a complete pipeline from passive data collection to validated treatment rankings, presented as both scientific methodology and implementation blueprint for next-generation regulatory systems.

Keywords: pharmacovigilance, real-world evidence, N-of-1 trials, pragmatic trials, causal inference, Bradford Hill criteria, treatment effects, validated outcome labels, comparative effectiveness, precision medicine

2 System Overview: From Methodology to Product

This paper describes the statistical methodology powering a patient-facing platform best understood as “Consumer Reports for drugs” - a searchable database where patients can look up any condition and see every treatment ranked by real-world effectiveness, with quantitative outcome labels showing exactly what happened to people who tried each option.

2.1 What Patients See

When a patient searches for their condition, they see:

Treatment Rankings: Every option (FDA-approved drugs, supplements, lifestyle interventions, experimental treatments) ranked by effect size from real patient data
Outcome Labels: “Nutrition facts for drugs” showing percent improvement, side effect rates, and sample sizes - not marketing claims
Trial Access: One-click enrollment in available trials, from home, via any device
Personalized Predictions: Based on their health data, which treatments work best for people like them

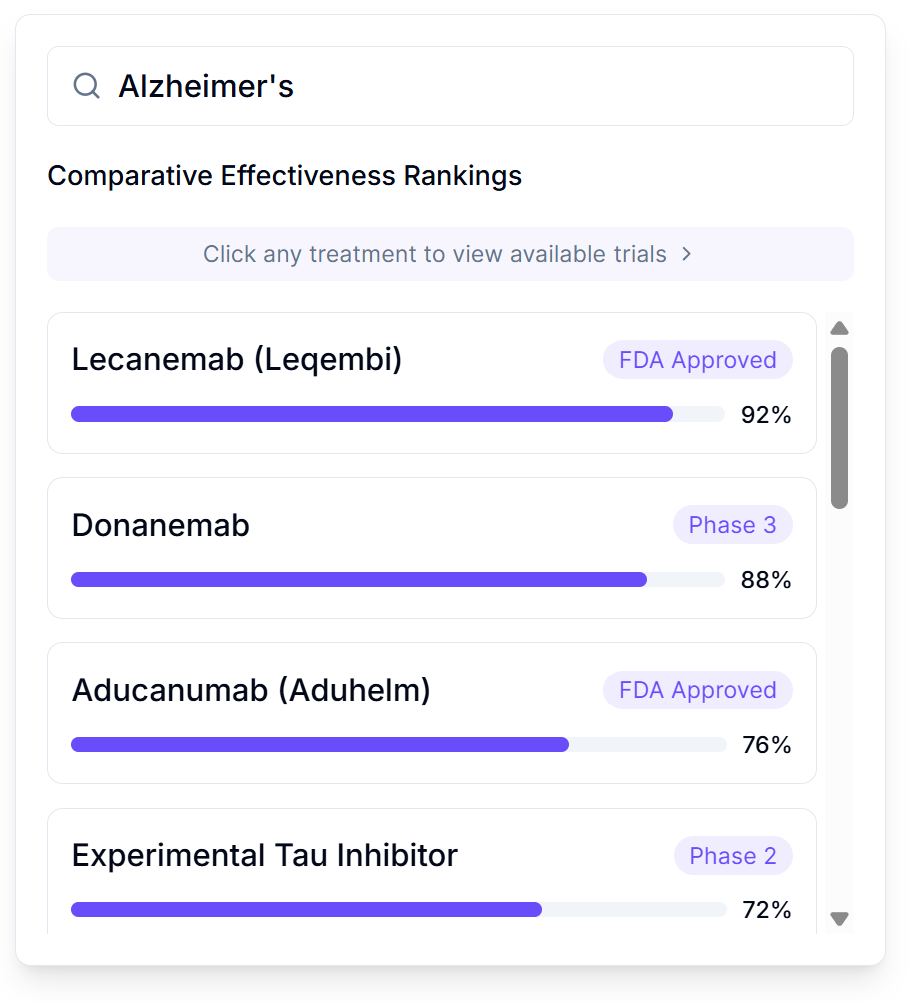
Figure 1: Treatment Rankings Example - Patients see all treatments ranked by real-world effectiveness for their condition

2.2 What Companies See

Any company - pharmaceutical, supplement, food, or intervention - can register a treatment in minutes at zero cost:

Instant Registration: No approval bottleneck; treatment appears in search results immediately
Zero Trial Cost: Patients pay for treatment (covering manufacturing); the platform handles data collection and analysis
Automatic Liability Coverage: Built into the platform
Free Clinical Data: Every patient who tries the treatment generates outcome data worth $41K (95% CI: $20K-$120K)/patient in traditional trials

2.3 Where This Methodology Fits

The Predictor Impact Score (PIS) described in this paper is the engine that powers treatment rankings. It transforms raw patient data into the ranked, quantified outcome labels that patients and clinicians use to make decisions. The two-stage pipeline ensures that:

Stage 1 (this methodology) generates treatment rankings from millions of real-world observations at ~$0.100 (95% CI: $0.030-$1.00)/patient
Stage 2 (pragmatic trials) confirms causation for high-priority signals at ~$500 (95% CI: $400-$2.50K)/patient

The result is a self-improving system where every patient’s experience helps the next patient make better decisions - transforming the current bottleneck of 1.90M patients/year (95% CI: 1.50M patients/year-2.30M patients/year) annual trial participants into a platform where anyone can contribute to medical knowledge.

For the complete user-facing vision, see A Decentralized Framework for Drug Assessment.

3 Introduction

3.1 The Human Cost of the Current System

Every year, 55.0M deaths/year (95% CI: 46.6M deaths/year-63.2M deaths/year) people die from diseases for which treatments exist or could exist. The tragedy is not that we lack medical knowledge. It’s that our system for generating and validating that knowledge operates at a fraction of its potential capacity.

Consider: a treatment that could save lives today takes an average of 8.2 years (95% CI: 4.85 years-11.5 years) to complete Phase 2-4 clinical trials after initial discovery. During this delay, people die waiting. Since 1962, regulatory testing delays for drugs that were eventually approved have contributed to an estimated 98.4M deaths (95% CI: 58.2M deaths-138M deaths) preventable deaths, more than all wars and conflicts of the 20th century combined.

This is not an argument against safety testing. It is an argument for better safety testing: faster, cheaper, more comprehensive, and continuously updated with real-world evidence rather than static pre-market snapshots.

The framework presented here could eliminate this efficacy lag for existing treatments while simultaneously enabling continuous discovery of new therapeutic relationships. The technology exists. The data exists. What remains is the institutional will to deploy it.

3.2 The Pharmacovigilance Gap

Modern pharmacovigilance (the science of detecting, assessing, and preventing adverse effects of pharmaceutical products) faces fundamental limitations:

Spontaneous Reporting Systems (e.g., FDA FAERS, EU EudraVigilance):

Estimated 1-10% of adverse events are reported¹²
No denominator data (cannot calculate incidence rates)
Cannot quantify effect sizes or establish causality
Significant reporting lag (months to years)
Subject to stimulated reporting and notoriety bias

Pre-Market Clinical Trials:

Limited sample sizes (typically hundreds to low thousands)
Short duration (weeks to months)
Homogeneous populations (exclusion criteria eliminate comorbidities)
Controlled conditions unlike real-world use
Cannot detect rare or delayed adverse events
Cost: Average Phase III trial costs $20M and takes 3+ years⁴

Post-Market Studies:

Expensive and time-consuming
Often industry-sponsored with potential conflicts
Limited to specific questions rather than comprehensive monitoring

3.3 The Real-World Data Opportunity

The past decade has seen explosive growth in patient-generated health data:

Wearable devices: 500+ million users globally tracking sleep, activity, heart rate¹³
Health apps: Symptom trackers, mood journals, medication reminders
Connected health platforms: Comprehensive longitudinal health records
Patient-reported outcomes: Systematic symptom and quality-of-life tracking

This data is characterized by:

Longitudinal structure: Repeated measurements over months to years
Natural variation: Patients modify treatments without experimental control
Real-world conditions: Actual usage patterns, not controlled settings
Scale: Millions of potential participants

3.4 Our Contribution

We present a framework that transforms real-world health data into actionable pharmacovigilance intelligence:

Quantitative Outcome Labels: For each treatment, generate effect sizes (percent change from baseline) for all measured outcomes
Treatment Rankings: Rank treatments by efficacy and safety within therapeutic categories
Automated Signal Detection: Identify safety concerns (negative correlations) and efficacy signals (positive correlations)
Bradford Hill Integration: Composite scoring that operationalizes causal inference criteria^14,15
Scalable Implementation: Analyze millions of treatment-outcome pairs automatically

This is not a replacement for RCTs but a complement, providing continuous, population-scale monitoring that can:

Generate hypotheses for experimental validation
Detect signals missed by spontaneous reporting
Quantify effects that RCTs can only describe qualitatively
Enable personalized benefit-risk assessment

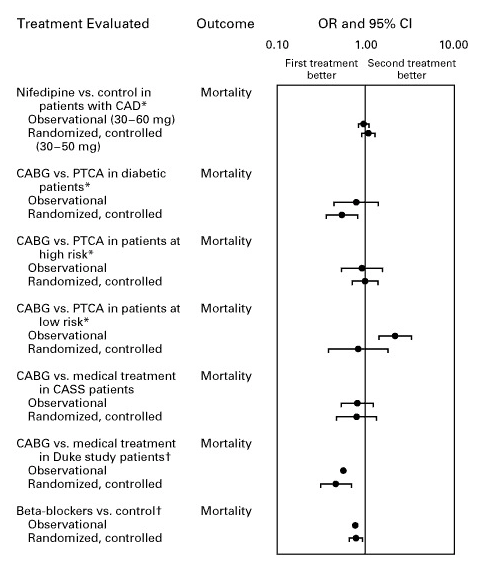
Multiple meta-analyses demonstrate that well-designed observational studies produce effect sizes concordant with randomized controlled trials, supporting the validity of real-world evidence for hypothesis generation:

Figure 2: Effect sizes from observational studies vs. randomized trials show strong concordance for mortality outcomes

Figure 3: Across multiple clinical domains, observational and randomized effect sizes track closely

4 Data Collection and Integration

4.1 Data Sources

Our framework integrates data from multiple sources, each contributing different variable types:

Source Category	Examples	Data Types
Wearables	Fitbit, Apple Watch, Oura Ring, Garmin	Sleep, steps, heart rate, HRV
Health Apps	Symptom trackers, mood journals	Symptoms, mood, energy, pain
Medication Trackers	Medisafe, MyTherapy	Drug intake, dosage, timing
Diet Trackers	MyFitnessPal, Cronometer	Foods, nutrients, calories
Lab Integrations	Quest, LabCorp APIs	Biomarkers, blood tests
EHR Connections	FHIR-enabled systems	Diagnoses, prescriptions, vitals
Manual Entry	Custom tracking	Any user-defined variable
Environmental	Weather APIs, air quality	Temperature, humidity, pollution

4.2 Variable Ontology

Variables are organized into semantic categories that inform default processing parameters:

Category	Examples	Onset Delay	Duration	Filling
Treatments	Drugs, supplements	30 min	24 hours	Zero
Foods	Diet, beverages	30 min	10 days	Zero
Symptoms	Pain, fatigue, nausea	0	24 hours	None
Emotions	Mood, anxiety, depression	0	24 hours	None
Vital Signs	Blood pressure, glucose	0	24 hours	None
Sleep	Duration, quality, latency	0	24 hours	None
Physical Activity	Steps, exercise, calories burned	0	24 hours	None
Environment	Weather, air quality, allergens	0	24 hours	None
Physique	Weight, body fat, measurements	0	7 days	None

4.3 Measurement Structure

Each measurement includes:

Measurement {
    variable_id: int           // Reference to variable definition
    user_id: int               // Anonymized participant identifier
    value: float               // Numeric measurement value
    unit_id: int               // Standardized unit reference
    start_time: timestamp      // When measurement was taken
    source_id: int             // Data source for provenance
    note: string (optional)    // User annotation
}

4.4 Unit Standardization

All measurements are converted to standardized units for cross-source compatibility:

Weights → kilograms
Distances → meters
Temperatures → Celsius
Dosages → milligrams
Durations → seconds
Percentages → 0-100 scale
Ratings → 1-5 scale (normalized)

5 Mathematical Framework

The short version: We track what people take (treatments, supplements, foods) and how they feel (symptoms, mood, energy) over time. Then we look for patterns: “When people take more of X, does Y get better or worse?” We account for the fact that treatments take time to work (onset delay) and their effects fade (duration of action). The math below makes this rigorous.

5.1 Data Structure

For each participant $i \in \{1, ..., N\}$, we observe time series of predictor variable $P$ (e.g., treatment) and outcome variable $O$ (e.g., symptom):

\[P_i = \{(t_{i,1}^P, p_{i,1}), (t_{i,2}^P, p_{i,2}), ..., (t_{i,n_i}^P, p_{i,n_i})\}\]

\[O_i = \{(t_{i,1}^O, o_{i,1}), (t_{i,2}^O, o_{i,2}), ..., (t_{i,m_i}^O, o_{i,m_i})\}\]

where $t$ denotes timestamp, $p$ denotes predictor measurements, and $o$ denotes outcome measurements. Critically, timestamps need not be aligned. Our framework handles asynchronous, irregular sampling.

5.2 Temporal Alignment

5.2.1 3.2.1 Onset Delay and Duration of Action

Treatments do not produce immediate effects. We define:

Onset delay $\delta$: Time lag before treatment produces observable effect
Duration of action $\tau$: Time window over which effect persists

Constraints: \[0 \leq \delta \leq 8{,}640{,}000 \text{ seconds (100 days)}\] \[600 \leq \tau \leq 7{,}776{,}000 \text{ seconds (90 days)}\]

5.2.2 3.2.2 Outcome Window Calculation

For a predictor measurement at time $t$, we associate it with outcome measurements in the window:

\[W(t) = \{t_j : t + \delta \leq t_j \leq t + \delta + \tau\}\]

The aligned outcome value is computed as the mean:

\[\bar{o}(t) = \frac{1}{|W(t)|} \sum_{t_j \in W(t)} o_j\]

5.3 Pair Generation Strategies

We employ two complementary strategies depending on variable characteristics:

5.3.1 3.3.1 Outcome-Based Pairing (Predictor has Filling Value)

When the predictor has a filling value (e.g., zero for “not taken”), we create one pair per outcome measurement:

For each outcome measurement (t_o, o):
    window_end = t_o - δ
    window_start = window_end - τ + 1

    predictor_values = measurements in [window_start, window_end]

    if predictor_values is empty:
        predictor_value = filling_value  // e.g., 0
    else:
        predictor_value = mean(predictor_values)

    create_pair(predictor_value, o)

5.3.2 3.3.2 Predictor-Based Pairing (No Filling Value)

When the predictor has no filling value, we create one pair per predictor measurement:

For each predictor measurement (t_p, p):
    window_start = t_p + δ
    window_end = window_start + τ - 1

    outcome_values = measurements in [window_start, window_end]

    if outcome_values is empty:
        skip this pair
    else:
        outcome_value = mean(outcome_values)
        create_pair(p, outcome_value)

5.4 Filling Value Logic

5.4.1 3.4.1 Filling Types

Type	Description	Use Case
Zero	Missing = 0	Treatments (assume not taken)
Value	Missing = specific constant	Known default states
None	No imputation	Continuous outcomes
Interpolation	Linear interpolation	Slowly-changing variables

5.4.2 3.4.2 Temporal Boundaries

To prevent spurious correlations from extended filling periods:

Earliest filling time: First recorded measurement (tracking start)
Latest filling time: Last recorded measurement (tracking end)

Pairs outside these boundaries are excluded. This prevents filling zeros for a treatment before the participant started tracking it.

5.4.3 3.4.3 Conservative Bias

Our filling strategy is deliberately conservative:

Zero-filling for treatments assumes non-adherence when no measurement exists
This biases toward null findings (attenuated correlations) rather than false positives
True effects must overcome this conservative bias to appear significant

5.5 Baseline Definition and Outcome Estimation

5.5.1 3.5.1 Within-Subject Comparison

For each participant $i$, we compute the mean predictor value:

\[\bar{p}_i = \frac{1}{n_i} \sum_{j=1}^{n_i} p_{i,j}\]

We partition measurements into baseline and follow-up periods:

\[\text{Baseline}_i = \{(p, o) : p < \bar{p}_i\}\] \[\text{Follow-up}_i = \{(p, o) : p \geq \bar{p}_i\}\]

This creates a natural within-subject comparison:

Baseline: Periods of below-average predictor exposure
Follow-up: Periods of above-average predictor exposure

5.5.2 3.5.2 Outcome Means

\[\mu_{\text{baseline},i} = \mathbb{E}[o \mid p < \bar{p}_i]\] \[\mu_{\text{follow-up},i} = \mathbb{E}[o \mid p \geq \bar{p}_i]\]

5.6 Percent Change from Baseline

The primary effect size metric:

\[\Delta_i = \frac{\mu_{\text{follow-up},i} - \mu_{\text{baseline},i}}{\mu_{\text{baseline},i}} \times 100\]

Advantages:

Interpretability: “15% reduction in pain” is intuitive
Scale invariance: Enables comparison across different outcome measures
Clinical relevance: Standard metric in medical literature
Regulatory familiarity: FDA uses percent change in efficacy assessments

5.7 Correlation Coefficients

We compute both parametric and non-parametric measures:

5.7.1 3.7.1 Pearson Correlation (Linear Relationships)

\[r_{\text{Pearson}} = \frac{\sum_{j=1}^{n}(p_j - \bar{p})(o_j - \bar{o})}{\sqrt{\sum_{j=1}^{n}(p_j - \bar{p})^2} \cdot \sqrt{\sum_{j=1}^{n}(o_j - \bar{o})^2}}\]

5.7.2 3.7.2 Spearman Rank Correlation (Monotonic Relationships)

\[r_{\text{Spearman}} = 1 - \frac{6 \sum_{j=1}^{n} d_j^2}{n(n^2 - 1)}\]

where $d_j = \text{rank}(p_j) - \text{rank}(o_j)$.

5.7.3 3.7.3 Forward and Reverse Correlations

We compute both:

Forward: $P \to O$ (predictor predicts outcome)
Reverse: $O \to P$ (outcome predicts predictor)

If reverse correlation is stronger, this suggests:

Reverse causality (symptom drives treatment-seeking)
Confounding by indication
Bidirectional relationship

5.8 Z-Score Normalization

To assess effect magnitude relative to natural variability:

\[z = \frac{|\Delta|}{\text{RSD}_{\text{baseline}}}\]

where relative standard deviation:

\[\text{RSD}_{\text{baseline}} = \frac{\sigma_{\text{baseline}}}{\mu_{\text{baseline}}} \times 100\]

Interpretation: $z > 2$ indicates $p < 0.05$ under normality, meaning the observed effect exceeds typical baseline fluctuation.

5.9 Statistical Significance

Two-tailed t-test for correlation significance:

\[t = \frac{r\sqrt{n-2}}{\sqrt{1-r^2}}\]

with $n-2$ degrees of freedom. Reject null hypothesis ($H_0: \rho = 0$) at $\alpha = 0.05$ when:

\[|t| > t_{\text{critical}}(n-2, \alpha/2)\]

5.10 Hyperparameter Optimization

The onset delay $\delta^*$ and duration of action $\tau^*$ are selected to maximize correlation coefficient strength:

\[(\delta^*, \tau^*) = \underset{\delta, \tau}{\text{argmax}} \; |r(\delta, \tau)|\]

Search Strategy: 1. Initialize with category defaults (e.g., 30 min onset, 24 hr duration for drugs) 2. Grid search over physiologically plausible ranges 3. Select parameters yielding strongest correlation coefficient

Overfitting Mitigation:

Restrict search to category-appropriate ranges
Require minimum sample size before optimization
Report both optimized and default-parameter results

6 Population Aggregation

6.1 Individual to Population

For population-level estimates, aggregate across $N$ participants:

\[\bar{r} = \frac{1}{N} \sum_{i=1}^{N} r_i\]

\[\bar{\Delta} = \frac{1}{N} \sum_{i=1}^{N} \Delta_i\]

6.2 Standard Error and Confidence Intervals

\[\text{SE}_{\bar{r}} = \frac{\sigma_r}{\sqrt{N}}\]

\[\text{CI}_{95\%} = \bar{r} \pm 1.96 \cdot \text{SE}_{\bar{r}}\]

6.3 Heterogeneity Assessment

Between-participant variance:

\[\sigma^2_{\text{between}} = \text{Var}(r_i)\]

High heterogeneity suggests:

Subgroup effects (responders vs. non-responders)
Interaction with unmeasured factors
Need for personalized analysis

7 Data Quality Requirements

7.1 Minimum Thresholds

Requirement	Threshold	Rationale
Predictor value changes	$\geq 5$	Ensures sufficient variance
Outcome value changes	$\geq 5$	Ensures sufficient variance
Overlapping pairs	$\geq 30$	Central limit theorem
Baseline fraction	$\geq 10\%$	Adequate baseline
Follow-up fraction	$\geq 10\%$	Adequate predictor exposure
Processed daily measurements	$\geq 4$	Minimum data density

7.2 Variance Validation

Before computing variable relationships, validate sufficient variance:

\[\text{changes}(X) = \sum_{j=1}^{n-1} \mathbb{1}[x_j \neq x_{j+1}]\]

If $\text{changes}(P) < 5$ or $\text{changes}(O) < 5$, abort with InsufficientVarianceException.

7.3 Outcome Value Spread

\[\text{spread}_O = \max(O) - \min(O)\]

Variable relationships with zero spread are undefined and excluded.

8 Predictor Impact Score

The short version: Not all correlations are created equal. If we observe that “people who take Drug X report less pain,” how confident should we be? The Predictor Impact Score (PIS) answers this by combining: (1) how strong is the relationship, (2) how many people show it, (3) does the drug come before the improvement (not after), and (4) is there a dose-response pattern. High PIS = worth investigating in a clinical trial. Low PIS = probably noise.

The Predictor Impact Score (PIS) is a composite metric that quantifies treatment-outcome relationship strength from patient health data, operationalizing Bradford Hill causality criteria to prioritize drug effects for clinical trial validation. It integrates correlation strength, statistical significance, effect magnitude, and multiple Bradford Hill criteria into a single interpretable score. Higher scores indicate predictors with greater, more reliable impact on the outcome.

Citation format: When citing this metric in academic work, use “Predictor Impact Score” with reference to this methodology document.

8.1 What Makes the Predictor Impact Score Novel

Unlike simple correlation coefficients, PIS addresses fundamental limitations of observational analysis:

Sample size agnosticism: Raw correlations don’t account for whether N=10 or N=10,000. PIS incorporates saturation functions that weight evidence accumulation.
Temporal ambiguity: Correlations can’t distinguish A→B from B→A. PIS includes a temporality factor comparing forward vs. reverse correlations.
Effect magnitude blindness: Statistical significance ≠ practical significance. PIS incorporates z-scores to assess effect magnitude relative to baseline variability.
Isolated metrics: Traditional analysis reports correlation, p-value, and effect size separately. PIS integrates them into a single prioritization metric aligned with Bradford Hill criteria.

The Predictor Impact Score is not a causal proof. It’s a principled heuristic for ranking which predictor-outcome relationships warrant further investigation, including experimental validation.

8.2 User-Level Predictor Impact Score

For individual participant (N-of-1) analyses, we compute:

\[\text{PIS}_{\text{user}} = |r| \cdot S \cdot \phi_z \cdot \phi_{\text{temporal}} \cdot f_{\text{interest}} + \text{PIS}_{\text{agg}}\]

Where:

$|r|$ = absolute value of the correlation coefficient (strength)
$S$ = statistical significance (1 - p-value)
$\phi_z$ = normalized z-score factor (effect magnitude)
$\phi_{\text{temporal}}$ = temporality factor (forward vs. reverse causation)
$f_{\text{interest}}$ = interest factor (penalizes spurious variable pairs)
$\text{PIS}_{\text{agg}}$ = population-level aggregate score (provides context from broader population)

8.3 Aggregate (Population-Level) Predictor Impact Score

For population-level analyses aggregated across multiple participants:

\[\text{PIS}_{\text{agg}} = |r_{\text{forward}}| \cdot w \cdot \phi_{\text{users}} \cdot \phi_{\text{pairs}} \cdot \phi_{\text{change}} \cdot \phi_{\text{gradient}}\]

Where:

$|r_{\text{forward}}|$ = absolute forward Pearson correlation coefficient (strength)
$w$ = weighted average of community votes on plausibility
$\phi_{\text{users}} = 1 - e^{-N / N_{\text{sig}}}$ (user saturation, $N_{\text{sig}} = 10$)
$\phi_{\text{pairs}} = 1 - e^{-n / n_{\text{sig}}}$ (pair saturation, $n_{\text{sig}}$ = significant pairs threshold)
$\phi_{\text{change}} = 1 - e^{-\Delta_{\text{spread}} / \Delta_{\text{sig}}}$ (change spread saturation)
$\phi_{\text{gradient}}$ = biological gradient coefficient (dose-response)

The saturation functions asymptotically approach 1 as sample sizes increase, reflecting that consistent findings across more participants strengthen causal inference.

8.4 Z-Score and Effect Magnitude Factor

The z-score quantifies the magnitude of the outcome change relative to baseline variability:

\[z = \frac{|\Delta\%_{\text{baseline}}|}{\text{RSD}_{\text{baseline}}}\]

Where:

$\Delta\%_{\text{baseline}}$ = percent change from baseline (see below)
$\text{RSD}_{\text{baseline}}$ = relative standard deviation of outcome during baseline period

A z-score > 2 indicates statistical significance (p < 0.05), meaning the observed change is unlikely due to random variation.

The normalized z-score factor incorporates effect magnitude into the PIS score:

\[\phi_z = \frac{|z|}{|z| + z_{\text{ref}}}\]

Where $z_{\text{ref}} = 2$ (the conventional significance threshold). This saturating function:

Approaches 0 for negligible effects (z → 0)
Equals 0.5 at the significance threshold (z = 2)
Approaches 1 for very large effects (z → ∞)

8.5 Temporality Factor

The temporality factor quantifies evidence that the predictor precedes and causes the outcome (rather than reverse causation):

\[\phi_{\text{temporal}} = \frac{|r_{\text{forward}}|}{|r_{\text{forward}}| + |r_{\text{reverse}}|}\]

Where:

$r_{\text{forward}}$ = correlation when predictor precedes outcome (P → O)
$r_{\text{reverse}}$ = correlation when outcome precedes predictor (O → P)

This factor:

Equals 0.5 when forward and reverse correlations are equal (ambiguous causality)
Approaches 1 when forward correlation dominates (supports predictor → outcome)
Approaches 0 when reverse correlation dominates (suggests reverse causation or confounding by indication)

8.6 Percent Change from Baseline

The primary effect size metric expressing treatment impact:

\[\Delta\%_{\text{baseline}} = \frac{\bar{O}_{\text{follow-up}} - \bar{O}_{\text{baseline}}}{\bar{O}_{\text{baseline}}} \times 100\]

Where:

$\bar{O}_{\text{follow-up}}$ = mean outcome value during follow-up period (after predictor exposure)
$\bar{O}_{\text{baseline}}$ = mean outcome value during baseline period (before predictor exposure)

For outcomes measured in percentages or with zero baseline, we use absolute change instead: \[\Delta_{\text{abs}} = \bar{O}_{\text{follow-up}} - \bar{O}_{\text{baseline}}\]

8.7 Statistical Significance

The statistical significance component captures confidence in the relationship:

\[S = 1 - p\]

Where $p$ is the p-value from the correlation significance test. Higher values indicate greater confidence that the observed relationship is not due to chance.

8.8 Interest Factor

The interest factor $f_{\text{interest}}$ penalizes likely spurious or uninteresting variable pairs:

\[f_{\text{interest}} = f_P \cdot f_O \cdot f_{\text{pair}}\]

Where:

$f_P$ = predictor interest factor (reduced for test variables, apps, addresses)
$f_O$ = outcome interest factor (reduced for non-outcome categories)
$f_{\text{pair}}$ = pair appropriateness (reduced for illogical category combinations)

8.9 Additional Data Quality Components

Skewness Coefficient (penalizes non-normal distributions): \[\phi_{\text{skew}} = \frac{1}{1 + \gamma_{P}^2} \cdot \frac{1}{1 + \gamma_{O}^2}\]

Kurtosis Coefficient (penalizes heavy tails): \[\phi_{\text{kurt}} = \frac{1}{1 + \kappa_{P}^2} \cdot \frac{1}{1 + \kappa_{O}^2}\]

Biological Gradient (dose-response relationship): \[\phi_{\text{gradient}} = \left(\frac{\bar{p}_{\text{high}} - \bar{p}}{\sigma_P} - \frac{\bar{p}_{\text{low}} - \bar{p}}{\sigma_P}\right)^2\]

Measures the standardized difference between predictor values that predict high vs. low outcomes.

8.10 Bradford Hill Criteria Mapping

The PIS operationalizes six of the nine Bradford Hill criteria for causality¹⁶:

Component	Formula	Bradford Hill Criterion	In PIS Formula
$\\|r\\|$	Correlation magnitude	Strength	Yes (direct)
$\phi_z$	Normalized z-score	Strength (effect magnitude)	Yes (user-level)
$\Delta\%$	Percent change from baseline	Strength (clinical significance)	Yes (via $\phi_z$)
$\phi_{\text{users}}, \phi_{\text{pairs}}$	Sample saturation	Consistency	Yes (aggregate)
$\phi_{\text{gradient}}$	Dose-response coefficient	Biological Gradient	Yes (aggregate)
$w$	Weighted community votes	Plausibility	Yes (aggregate)
$f_{\text{interest}}$	Category appropriateness	Specificity	Yes (user-level)
$\phi_{\text{temporal}}$	Forward/reverse ratio	Temporality	Yes (user-level)
$\delta > 0$	Onset delay requirement	Temporality	Enforced in design

8.11 Interpreting Predictor Impact Scores

PIS scores range from 0 to approximately 1 (though values slightly above 1 are possible with very strong evidence). Guidelines for interpretation:

PIS Range	Interpretation	Recommended Action
≥ 0.5	Strong evidence	High priority for RCT validation
0.3 - 0.5	Moderate evidence	Consider for experimental investigation
0.1 - 0.3	Weak evidence	Monitor for additional data
< 0.1	Insufficient evidence	Low priority; may be noise

Important caveats:

These thresholds are preliminary and should be validated against RCT outcomes
PIS is relative, not absolute. Use it for prioritization, not proof.
High PIS does not guarantee causation; low PIS does not rule it out
Context matters: a PIS of 0.2 for a novel relationship may be more interesting than 0.5 for a known one

8.12 Optimal Daily Value for Precision Dosing

A key output of our analysis is the optimal daily value, the predictor value that historically precedes the best outcomes. This enables personalized, precision dosing recommendations.

8.12.1 6.11.1 Value Predicting High Outcome

The Value Predicting High Outcome ($V_{\text{high}}$) is the average predictor value observed when the outcome exceeds its mean:

\[V_{\text{high}} = \frac{1}{|H|} \sum_{(p, o) \in H} p\]

Where:

$H = \{(p, o) : o > \bar{O}\}$ is the set of predictor-outcome pairs where outcome exceeds its average
$\bar{O}$ = mean outcome value across all pairs
$p$ = predictor (cause) value for each pair

Calculation Process: 1. Compute the average outcome value ($\bar{O}$) across all predictor-outcome pairs 2. Filter pairs to include only those where outcome > $\bar{O}$ (the “high effect” pairs) 3. Calculate the mean predictor value across these high-effect pairs

8.12.2 6.11.2 Value Predicting Low Outcome

The Value Predicting Low Outcome ($V_{\text{low}}$) is the average predictor value observed when the outcome is below its mean:

\[V_{\text{low}} = \frac{1}{|L|} \sum_{(p, o) \in L} p\]

Where:

$L = \{(p, o) : o < \bar{O}\}$ is the set of predictor-outcome pairs where outcome is below its average

8.12.3 6.11.3 Grouped Optimal Values

For interpretability, we also calculate grouped optimal values that map to common dosing intervals:

Grouped Value Predicting High Outcome: The nearest grouped predictor value (e.g., rounded to typical dosing units) to $V_{\text{high}}$
Grouped Value Predicting Low Outcome: The nearest grouped predictor value to $V_{\text{low}}$

This allows recommendations like “400mg of Magnesium” rather than “412.7mg of Magnesium.”

8.12.4 6.11.4 Precision Dosing Recommendations

These optimal values enable personalized recommendations:

For Positive Valence Outcomes (where higher is better, e.g., energy, sleep quality): > “Your [Outcome] was highest after [Grouped Value Predicting High Outcome] of [Predictor] over the previous [Duration of Action].” > > Example: “Your Sleep Quality was highest after 400mg of Magnesium over the previous 24 hours.”

For Negative Valence Outcomes (where lower is better, e.g., pain, anxiety): > “Your [Outcome] was lowest after [Grouped Value Predicting Low Outcome] of [Predictor] over the previous [Duration of Action].” > > Example: “Your Anxiety Severity was lowest after 100mg of Sertraline over the previous 24 hours.”

8.12.5 6.11.5 Mathematical Relationship to Biological Gradient

The optimal values are closely related to the biological gradient coefficient ($\phi_{\text{gradient}}$):

\[\phi_{\text{gradient}} = \left(\frac{V_{\text{high}} - \bar{P}}{\sigma_P} - \frac{V_{\text{low}} - \bar{P}}{\sigma_P}\right)^2\]

A larger separation between $V_{\text{high}}$ and $V_{\text{low}}$ indicates:

Stronger dose-response relationship
More reliable precision dosing recommendations
Higher biological gradient coefficient

8.12.6 6.11.6 Clinical Applications

Metric	Definition	Clinical Use
$V_{\text{high}}$	Avg predictor when outcome > mean	Optimal dose for positive outcomes
$V_{\text{low}}$	Avg predictor when outcome < mean	Dose to avoid for positive outcomes
$V_{\text{high}} - V_{\text{low}}$	Optimal value spread	Magnitude of dose-response effect

Example Application: For a participant tracking Magnesium supplementation and Sleep Quality:

$V_{\text{high}}$ = 412mg → Grouped = 400mg (sleep quality highest after this dose)
$V_{\text{low}}$ = 127mg → Grouped = 125mg (sleep quality lowest after this dose)
Recommendation: “Take approximately 400mg of Magnesium for optimal sleep quality”

8.12.7 6.11.7 Limitations

Correlation ≠ Causation: Optimal values reflect associations, not guaranteed causal effects
Individual Variation: Population optimal values may not be optimal for all individuals
Context Dependence: Optimal values may vary by timing, combination with other factors
Grouping Artifacts: Rounding to common doses may lose precision

Best Practice: Use optimal values as starting points for personal experimentation, not as definitive prescriptions.

8.12.8 6.11.8 Confidence Intervals for Optimal Values

Optimal values should be reported with uncertainty bounds to convey reliability:

\[\text{CI}_{V_{\text{high}}} = V_{\text{high}} \pm t_{\alpha/2} \cdot \frac{\sigma_{p|H}}{\sqrt{|H|}}\]

Where:

$\sigma_{p|H}$ = standard deviation of predictor values in high-outcome set $H$
$|H|$ = number of pairs in high-outcome set
$t_{\alpha/2}$ = critical t-value for desired confidence level

Interpretation Guidelines:

CI Width (relative to mean)	Reliability	Recommendation
< 10%	High	Use as primary recommendation
10-25%	Moderate	Present as range (e.g., “350-450mg”)
25-50%	Low	Insufficient precision for dosing
> 50%	Very Low	Do not use for recommendations

Example: If $V_{\text{high}} = 400\text{mg}$ with 95% CI [380, 420], report: “Optimal dose: 400mg (95% CI: 380-420mg)”

8.12.9 6.11.9 Individual vs Population Optimal Values

Both individual and population optimal values are computed and stored. Guidelines for use:

Scenario	Recommended Source	Rationale
User has ≥50 paired measurements	Individual $V_{\text{high}}$	Sufficient personal data
User has 20-50 measurements	Weighted blend	$0.5 \cdot V_{\text{user}} + 0.5 \cdot V_{\text{pop}}$
User has <20 measurements	Population $V_{\text{high}}$	Insufficient personal data
User’s optimal differs >50% from population	Flag for review	May indicate unique response or data quality issue

Blending Formula:

\[V_{\text{recommended}} = w \cdot V_{\text{user}} + (1-w) \cdot V_{\text{pop}}\]

Where $w = \min(1, n_{\text{user}} / n_{\text{threshold}})$ with $n_{\text{threshold}} = 50$ pairs.

8.12.10 6.11.10 Temporal Stability and Recalculation

Optimal values may drift over time due to:

Physiological changes (age, weight, health status)
Tolerance development
Seasonal factors
Lifestyle changes

Recalculation Policy:

Trigger	Action
New measurements added	Recalculate after every 10 new pairs
Time elapsed	Recalculate monthly regardless of new data
Significant life change	User-triggered recalculation
Optimal value drift >20%	Alert user to potential change

Rolling Window Option: For treatments where tolerance is expected, compute optimal values using only the most recent 90 days of data rather than all historical data.

Stability Metric: \[\text{Stability} = 1 - \frac{|V_{\text{high}}^{\text{current}} - V_{\text{high}}^{\text{previous}}|}{V_{\text{high}}^{\text{previous}}}\]

Stability < 0.8 (>20% change) triggers a notification to the user.

8.12.11 6.11.11 Edge Cases: Minimal Dose-Response

When $V_{\text{high}} \approx V_{\text{low}}$, the predictor shows no clear dose-response relationship:

Detection Criterion: \[\frac{|V_{\text{high}} - V_{\text{low}}|}{\sigma_P} < 0.5\]

(Less than half a standard deviation apart)

Possible Interpretations: 1. Threshold effect: Any dose above zero works equally well 2. No effect: Predictor doesn’t influence outcome 3. Non-linear response: U-shaped or inverted-U curve not captured by simple high/low split 4. Insufficient variance: User takes similar doses, preventing detection

Handling:

Do not display optimal value recommendations when dose-response is minimal
Instead report: “No clear dose-response relationship detected for [Predictor] → [Outcome]”
Flag for potential non-linear analysis in future versions

8.12.12 6.11.12 Validation of Optimal Values

The Critical Question: Do users who follow optimal value recommendations actually experience better outcomes than those who don’t?

Proposed Validation Study:

Prospective A/B Test:
- Group A: Receives personalized optimal value recommendations
- Group B: Receives no recommendations (continues current behavior)
- Compare outcome trajectories over 30-90 days
Retrospective Adherence Analysis:
- For users with established optimal values, calculate “adherence score”: \[\text{Adherence} = \frac{\text{Days within } \pm 20\% \text{ of } V_{\text{high}}}{\text{Total tracking days}}\]
- Correlate adherence with outcome improvement

Success Metrics:

Users in top adherence quartile should show >15% better outcomes than bottom quartile
Optimal value recommendations should outperform random dosing by >10%

Current Status: This validation has not been performed. Until validated, optimal values should be presented as “data-driven suggestions” rather than “clinically validated recommendations.”

8.13 Saturation Constant Rationale

The saturation constants (N_sig, n_sig, etc.) reflect pragmatic thresholds based on statistical and clinical considerations:

Constant	Value	Rationale
N_sig (users)	10	At N=10, user saturation ≈ 0.63. By N=30, ≈ 0.95. Reflects that consistency across 10+ individuals provides meaningful replication.
n_sig (pairs)	100	Central limit theorem suggests n≥30 for normality. We use 100 as the “strong evidence” threshold.
Δ_sig (change spread)	10%	A 10% change is often considered clinically meaningful across many health outcomes.
z_ref	2	Corresponds to p < 0.05 under normality (the conventional significance threshold).

These constants are not empirically optimized. Future work should: 1. Validate constants against known causal relationships (from RCTs) 2. Consider domain-specific thresholds (e.g., psychiatric vs. cardiovascular outcomes) 3. Implement sensitivity analyses to assess robustness to constant choices

8.14 Effect Following High vs Low Predictor Values

Beyond optimal values, we calculate the average outcome following different predictor levels to quantify dose-response relationships:

8.14.1 6.13.1 Average Outcome Metrics

Metric	Definition	Clinical Interpretation
Average Outcome	Mean outcome across all pairs	Baseline outcome level
Average Outcome Following High Predictor	Mean outcome when predictor > mean	Outcome after high exposure
Average Outcome Following Low Predictor	Mean outcome when predictor < mean	Outcome after low exposure
Average Daily High Predictor	Mean predictor in upper 51% of spread	“High dose” value
Average Daily Low Predictor	Mean predictor in lower 49% of spread	“Low dose” value

8.14.2 6.13.2 Calculation

\[\bar{O}_{\text{high}} = \mathbb{E}[O \mid P > \bar{P}]\] \[\bar{O}_{\text{low}} = \mathbb{E}[O \mid P \leq \bar{P}]\]

Where $\bar{P}$ is the mean predictor value across all pairs.

Effect Size from High to Low Cause: \[\Delta_{\text{high-low}} = \frac{\bar{O}_{\text{high}} - \bar{O}_{\text{low}}}{\bar{O}_{\text{low}}} \times 100\]

This metric directly shows the percent difference in outcome between high and low predictor exposure periods.

8.15 Predictor Baseline and Treatment Averages

For treatment-response analysis, we distinguish between baseline (non-treatment) and treatment periods:

Metric	Definition	Use Case
Predictor Baseline Average Per Day	Average daily predictor during low-exposure periods	Typical non-treatment value
Predictor Treatment Average Per Day	Average daily predictor during high-exposure periods	Typical treatment dosage
Predictor Baseline Average Per Duration Of Action	Baseline cumulative over duration of action	For longer-acting effects
Predictor Treatment Average Per Duration Of Action	Treatment cumulative over duration of action	Cumulative treatment dose

Example: For a user taking Magnesium supplements:

predictor_baseline_average_per_day = 50mg (days not supplementing, dietary only)
predictor_treatment_average_per_day = 400mg (days actively supplementing)
This reveals the effective treatment dose vs. background exposure

8.16 Relationship Quality Filters

Not all statistically significant relationships are useful. We apply quality filters to prioritize actionable findings:

8.16.1 6.15.1 Filter Flags

Flag	Description	Impact on Ranking
Predictor Is Controllable	User can directly modify this predictor (e.g., food, supplements)	Required for actionable recommendations
Outcome Is A Goal	Outcome is something users want to optimize (e.g., mood, energy)	Required for relevance
Plausibly Causal	Plausible biological mechanism exists	Increases confidence
Obvious	Relationship is already well-known (e.g., caffeine → alertness)	May deprioritize for discovery
Boring	Relationship unlikely to interest users	Filters from default views
Interesting Variable Category Pair	Category combination is typically meaningful (e.g., Treatment → Symptom)	Prioritizes for analysis

8.16.2 6.15.2 Boring Relationship Definition

A relationship is marked boring = TRUE if ANY of:

Predictor is not controllable AND outcome is not a goal
Relationship could not plausibly be causal
Confidence level is LOW
Effect size is negligible (|Δ| < 1%)
Relationship is trivially obvious

8.16.3 6.15.3 Usefulness and Causality Voting

Users can vote on individual relationships:

Vote Type	Values	Purpose
Usefulness Vote	-1, 0, 1	Whether knowledge of this relationship is useful
Causality Vote	-1, 0, 1	Whether there’s a plausible causal mechanism

Aggregate votes contribute to the PIS plausibility weight ($w$).

8.17 Variable Valence

Valence indicates whether higher values of a variable are inherently good, bad, or neutral:

Valence	Meaning	Examples
Positive	Higher is better	Energy, Sleep Quality, Productivity
Negative	Lower is better	Pain, Anxiety, Fatigue
Neutral	Direction depends on context	Heart Rate, Weight

8.17.1 6.16.1 Impact on Interpretation

Valence affects how we interpret correlation direction:

Predictor-Outcome Valence	Positive Correlation	Negative Correlation
Positive → Positive	Both improve together	Trade-off
Positive → Negative	Predictor worsens outcome	Predictor improves outcome
Treatment → Negative Symptom	Side effect	Therapeutic effect

Example: A positive correlation between Sertraline and Depression Severity is BAD (depression has negative valence, so lower is better). The same positive correlation between Sertraline and Energy would be GOOD.

8.18 Temporal Parameter Optimization

We optimize onset_delay (δ) and duration_of_action (τ) to find the temporal parameters that maximize correlation strength:

8.18.1 6.17.1 Stored Optimization Data

Field	Description
Correlations Over Delays	Pearson r values for various onset delays
Correlations Over Durations	Pearson r values for various durations of action
Onset Delay With Strongest Pearson Correlation	Optimal δ value
Pearson Correlation With No Onset Delay	Baseline r for immediate effect
Average Forward Pearson Correlation Over Onset Delays	Mean r across all tested delays
Average Reverse Pearson Correlation Over Onset Delays	Mean reverse r across delays

8.18.2 6.17.2 Optimization Grid

For each predictor-outcome pair, we test:

Onset delays: 0, 30min, 1hr, 2hr, 4hr, 8hr, 12hr, 24hr, 48hr, 72hr…
Durations: 1hr, 4hr, 12hr, 24hr, 48hr, 72hr, 1 week, 2 weeks…

The parameters yielding the strongest |r| are selected, subject to category-specific physiological constraints.

8.18.3 6.17.3 Overfitting Protection

To prevent spurious optimization: 1. Minimum pairs required: Only optimize if n > 50 pairs 2. Category constraints: Limit search to plausible ranges (e.g., caffeine onset < 2hr) 3. Report both: Show optimized AND default-parameter results 4. Consistency check: Compare forward vs reverse optimization

8.19 Spearman Rank Correlation

In addition to Pearson correlation, we compute Spearman rank correlation (forward_spearman_correlation_coefficient) for robustness:

\[r_s = 1 - \frac{6 \sum d_i^2}{n(n^2-1)}\]

Where $d_i$ = difference in ranks for each pair.

Advantages over Pearson:

Robust to outliers
Captures monotonic (not just linear) relationships
Less affected by skewed distributions

When to prefer Spearman:

Outcome has skewed distribution (e.g., symptom severity with many zeros)
Relationship is monotonic but non-linear (e.g., diminishing returns)
Data contains outliers from measurement errors

9 Outcome Label Generation

9.1 Predictor Analysis Reports

For each outcome variable (e.g., Depression Severity), we generate comprehensive “outcome labels” showing:

All predictors ranked by effect size
Positive predictors (treatments/factors that improve the outcome)
Negative predictors (treatments/factors that worsen the outcome)
Effect sizes as percent change from baseline
Confidence levels and sample sizes

9.2 Report Structure

Outcome Label: [Outcome Variable Name]
Population: N = [number] participants
Total Studies: [number] treatment-outcome pairs analyzed

POSITIVE EFFECTS (Treatments predicting IMPROVEMENT)
================================================
Rank | Treatment | Effect Size | 95% CI | N | Confidence
-----|-----------|-------------|--------|---|------------
1    | Treatment A | +23.5% | [18.2, 28.8] | 1,247 | High
2    | Treatment B | +18.2% | [12.1, 24.3] | 892 | High
3    | Treatment C | +12.7% | [8.3, 17.1] | 2,103 | High
...

NEGATIVE EFFECTS (Treatments predicting WORSENING)
=================================================
Rank | Treatment | Effect Size | 95% CI | N | Confidence
-----|-----------|-------------|--------|---|------------
1    | Treatment X | -15.3% | [-20.1, -10.5] | 567 | Medium
2    | Treatment Y | -8.7% | [-12.3, -5.1] | 1,892 | High
...

NO SIGNIFICANT EFFECT
=====================
[List of treatments with |Δ| < threshold or p > 0.05]

9.3 Category-Specific Analysis

Reports are organized by predictor category:

Treatments (Drugs, Supplements)
- Ranked by efficacy (positive Δ)
- Safety signals highlighted (negative Δ)
Foods & Nutrients
- Dietary factors affecting outcome
Lifestyle Factors
- Sleep, exercise, activities
Environmental Factors
- Weather, pollution, allergens
Comorbid Conditions
- Other symptoms/conditions as predictors

9.4 Verification Status

Each study is classified by verification status:

Status	Icon	Description
Verified	✓	Up-voted by users; data reviewed and valid
Unverified	?	Awaiting review
Flagged	✗	Down-voted; potential data quality issues

9.5 Outcome Labels vs. FDA Drug Labels

Traditional FDA drug labels are per-drug documents that list qualitative adverse events and indications based on pre-market trials. They are static (updated infrequently), qualitative (“may cause drowsiness”), and organized around the drug rather than the patient’s condition.

Outcome Labels invert this paradigm: they are per-outcome documents that rank all treatments by quantitative effect size for a given health outcome. They are dynamic (updated continuously as data arrives), quantitative (“↓24.7% depression severity”), and organized around what the patient wants to optimize. This enables patients and clinicians to answer the question: “What works best for my condition?” This is a question traditional drug labels cannot answer.

9.6 Worked Example: Complete Outcome Label

Figure 4: Outcome Labels show quantitative effect sizes, sample sizes, and confidence intervals for each treatment - like “nutrition facts for drugs”

The following shows a complete outcome label for depression, demonstrating how treatments are ranked by effect size with confidence intervals:

OUTCOME LABEL: Depression Severity

Based on 47,832 participants tracking depression outcomes Last updated: 2026-01-04 | Data period: 2020-2026

Treatments Improving Depression (ranked by effect size $\Delta$)

Table 1: Treatments associated with depression improvement. Negative effect indicates symptom reduction.

Rank	Treatment	Effect	95% CI	N	PIS	Optimal Dose
1	Exercise	−31.2%	[27.1, 35.3]	12,847	0.67	45 min/day
2	Bupropion	−28.3%	[22.1, 34.5]	2,847	0.54	300mg
3	Sertraline	−24.7%	[19.8, 29.6]	5,123	0.51	100mg
4	Sleep (7-9 hrs)	−22.1%	[18.4, 25.8]	31,204	0.48	8.2 hrs
5	Venlafaxine	−21.2%	[15.3, 27.1]	1,892	0.44	150mg
6	Omega-3	−18.9%	[14.2, 23.6]	4,521	0.38	2000mg EPA+DHA
7	Meditation	−16.4%	[12.1, 20.7]	8,932	0.35	20 min/day
8	Fluoxetine	−15.8%	[11.2, 20.4]	3,456	0.33	40mg
9	Vitamin D	−12.3%	[8.7, 15.9]	6,789	0.28	4000 IU
10	Social interaction	−11.7%	[8.2, 15.2]	9,234	0.26	3+ hrs/day

Treatments Worsening Depression (safety signals)

Table 2: Treatments associated with depression worsening. Positive effect indicates symptom increase.

Rank	Treatment	Effect	95% CI	N	PIS	Note
1	Alcohol (>2/day)	+23.4%	[18.9, 27.9]	7,234	0.52	Dose-dependent
2	Sleep deprivation	+19.8%	[15.2, 24.4]	14,521	0.47	<6 hrs/night
3	Social isolation	+15.2%	[11.3, 19.1]	5,892	0.38	<1 hr/day
4	Refined sugar	+8.7%	[5.2, 12.2]	11,234	0.24	>50g/day

No Significant Effect ($|\Delta| < 5\%$ or $p > 0.05$): Multivitamin, Probiotics, B-complex, Magnesium (for depression specifically), Ashwagandha, 5-HTP, SAMe, St. John’s Wort¹

Legend: PIS = Predictor Impact Score (0-1 scale, higher = stronger evidence); Optimal Dose = $V_{high}$ (predictor value associated with best outcomes)

Interpretation: This outcome label shows that for depression, exercise and sleep optimization rival or exceed pharmaceutical interventions in effect size, with stronger evidence bases (higher N). Bupropion and Sertraline lead among medications. The safety signals section highlights modifiable risk factors that worsen depression.

10 Treatment Ranking System

10.1 Within-Category Rankings

For each therapeutic category (e.g., Antidepressants), treatments are ranked by:

Primary: Effect size (percent change from baseline)
Secondary: Confidence level (High > Medium > Low)
Tertiary: Sample size

10.2 Ranking Algorithm

For each treatment $T$ in a therapeutic category, we compute a composite ranking score:

\[\text{RankScore}_T = \bar{\Delta}_T \times w_{\text{confidence}} \times \text{PIS}_T\]

where $\bar{\Delta}_T$ is the mean effect size across participants, $w_{\text{confidence}}$ is the confidence weight (see Table 3), and $\text{PIS}_T$ is the Predictor Impact Score. Treatments are sorted by descending rank score.

10.3 Confidence Weighting

Table 3: Confidence weighting schema for treatment ranking.

Confidence Level	Weight ($w$)	Criteria
High	1.0	$p < 0.01$ OR $N > 100$ OR pairs $> 500$
Medium	0.7	$p < 0.05$ OR $N > 10$ OR pairs $> 100$
Low	0.4	Meets minimum thresholds only

10.4 Comparative Effectiveness Display

Table 4 illustrates how treatments within a therapeutic category are presented to users.

Table 4: Antidepressants ranked by efficacy for depression. Negative effect indicates symptom reduction.

Rank	Treatment	Effect ($\Delta$)	95% CI	N	Confidence
1	Bupropion 300mg	−28.3%	[22.1, 34.5]	2,847	High
2	Sertraline 100mg	−24.7%	[19.8, 29.6]	5,123	High
3	Venlafaxine 150mg	−21.2%	[15.3, 27.1]	1,892	High
4	Fluoxetine 40mg	−18.9%	[13.2, 24.6]	3,456	High

11 Safety and Efficacy Quantification

11.1 Safety Signal Detection

Adverse Effect Identification: Safety signals are identified through (1) negative correlations between treatment and beneficial outcomes, and (2) positive correlations between treatment and harmful outcomes.

Table 5: Example safety signal report showing potential adverse effects with statistically significant positive correlations to harmful outcomes.

Outcome	Effect ($\Delta$)	95% CI	Plausibility	Action
Fatigue	+18.3%	[12.1, 24.5]	High (known sedation)	Monitor
Nausea	+15.7%	[8.9, 22.5]	High (GI effects)	Monitor
Weight Gain	+8.2%	[4.1, 12.3]	Medium	Long-term monitoring
Anxiety	+6.5%	[2.1, 10.9]	Low (paradoxical)	Investigate

11.2 Efficacy Signal Detection

Therapeutic Effect Identification: Efficacy signals are identified through (1) positive correlations between treatment and beneficial outcomes, and (2) negative correlations between treatment and harmful outcomes (symptom reduction).

Table 6: Example efficacy signal report showing therapeutic effects with statistically significant correlations.

Outcome	Effect ($\Delta$)	95% CI	Indication	Evidence
Depression	−24.7%	[19.8, 29.6]	Primary	Strong
Anxiety	−18.2%	[12.3, 24.1]	Secondary	Strong
Sleep Quality	+15.3%	[10.1, 20.5]	Secondary	Moderate
Energy	+12.1%	[7.2, 17.0]	Secondary	Moderate

11.3 Benefit-Risk Assessment

Net Clinical Benefit Score:

\[\text{NCB} = \sum_{i \in \text{benefits}} w_i \cdot |\Delta_i| - \sum_{j \in \text{risks}} w_j \cdot |\Delta_j|\]

where $w$ represents importance weights assigned by clinical relevance.

Example: Sertraline 100mg Benefit-Risk Profile

Table 7: Benefit-risk components for Sertraline 100mg.

Benefits	Effect	Weight	Risks	Effect	Weight
Depression	−24.7%	1.0	Nausea	+8.3%	0.3
Anxiety	−18.2%	0.8	Insomnia	+5.1%	0.4
			Sexual dysfunction	+12.7%	0.5

Weighted Summary: Benefits = 39.26, Risks = 8.93, Net Clinical Benefit = +30.33 (favorable profile for depression/anxiety)

12 Addressing the Bradford Hill Criteria

The Bradford Hill criteria¹⁶ provide the foundational framework for assessing causation from observational data. This section details how our framework addresses each criterion.

12.1 Complete Criteria Mapping

Criterion	How Addressed	Quantitative Metric	In PIS?
Strength	Effect size magnitude	Pearson $r$, $\Delta$%	Yes
Consistency	Cross-participant aggregation	$N$, $n$, SE, CI	Yes
Specificity	Category appropriateness	Interest factor	Yes
Temporality	Onset delay requirement	$\delta > 0$ enforced	Yes
Biological Gradient	Dose-response analysis	Gradient coefficient	Yes
Plausibility	Community voting	Up/down votes	Yes
Coherence	Literature cross-reference	Narrative	No
Experiment	N-of-1 natural experiments	Study design	No
Analogy	Similar variable comparison	Narrative	No

12.2 Quantitative Criteria Details

Strength:

Reports Pearson $r$ with classification (very strong: ≥0.8, strong: ≥0.6, moderate: ≥0.4, weak: ≥0.2, very weak: <0.2)
Example: “There is a moderately positive (R = 0.45) relationship between Sertraline and Depression improvement.”

Consistency:

Reports $N$ participants, $n$ paired measurements
Notes that spurious associations naturally dissipate as participants modify behaviors based on non-replicating findings

Temporality:

Onset delay $\delta$ explicitly encodes treatment-to-effect lag
Forward vs. reverse correlation comparison identifies potential reverse causality

Plausibility:

Users vote on biological mechanism plausibility
Weighted average contributes to ranking
Crowd-sources expert and patient knowledge

13 Validation and Quality Assurance

13.1 User Voting System

Each study can receive user votes:

Vote	Meaning	Effect
Up-vote (👍)	Data appears valid, relationship plausible	Included in verified results
Down-vote (👎)	Data issues or implausible relationship	Flagged for review
No vote	Not yet reviewed	Included in unverified results

13.2 Automated Quality Checks

Before inclusion in reports:

Variance check: Minimum 5 value changes in both variables
Sample size check: Minimum 30 paired measurements
Baseline adequacy: ≥10% of data in baseline period
Effect spread check: Non-zero outcome variance
Temporal coverage: Adequate follow-up duration

13.3 Flagged Study Handling

Studies may be flagged for:

Insufficient data
Extreme outliers
Implausible effect sizes (>200% change)
Data entry errors
Measurement device malfunctions

Flagged studies are:

Excluded from primary rankings
Available for review in separate section
Can be un-flagged after data correction

14 Stage 2: Pragmatic Trial Confirmation

The short version: Observational data can find promising signals, but only randomized trials can prove causation. The good news: we don’t need expensive, slow traditional trials. The Oxford RECOVERY trial proved that “pragmatic” trials (simple randomization embedded in routine care) can validate treatments at 82x (95% CI: 50x-94.1x) lower cost and 10x faster. We use cheap observational analysis (Stage 1) to filter millions of possibilities down to the top candidates, then confirm the best ones with pragmatic trials (Stage 2). Result: validated treatment recommendations at a fraction of current cost.

The observational methodology described in Sections 1-11 generates ranked hypotheses about treatment-outcome relationships. While powerful for signal detection and hypothesis generation, observational data alone cannot establish causation due to unmeasured confounding. This section describes how pragmatic clinical trials serve as the confirmation layer, transforming promising observational signals into validated causal relationships.

14.1 The Two-Stage Pipeline

Our complete methodology operates as a two-stage pipeline:

Stage	Method	Cost	Purpose	Output
Stage 1: Signal Detection	Aggregated N-of-1 observational analysis	~$0.10/patient	Hypothesis generation	Ranked PIS signals
Stage 2: Causal Confirmation	Pragmatic randomized trials	~$500 (95% CI: $400-$2.50K)/patient	Causation proof	Validated effect sizes

This design leverages the complementary strengths of each approach:

Stage 1 scales to millions of treatment-outcome pairs at minimal cost, identifying the most promising candidates
Stage 2 applies experimental rigor to confirm causation for high-priority signals

Figure 5: FDA vs dFDA: The two-stage pipeline dramatically reduces cost and time compared to traditional drug development

14.2 Pragmatic Trial Methodology

Pragmatic trials differ fundamentally from traditional Phase III trials¹⁰:

Dimension	Traditional Phase III	Pragmatic Trial (RECOVERY Model)
Cost per patient	$41K (95% CI: $20K-$120K)	$500 (95% CI: $400-$2.50K)
Time to results	3-7 years	3-6 months
Patient population	Homogeneous (strict exclusion)	Real-world (minimal exclusion)
Setting	Specialized research centers	Routine clinical care
Data collection	Extensive case report forms	Minimal essential outcomes
Randomization	Complex stratification	Simple 1:1 or 1:1:1
Sample size	Hundreds to thousands	Thousands to tens of thousands

The Oxford RECOVERY trial demonstrated this model’s effectiveness: 49,000 patients enrolled across 186 hospitals, 12 treatments evaluated, first life-saving result (dexamethasone) in 100 days, 1.00M lives (95% CI: 500k lives-2.00M lives) saved globally⁶.

14.3 Signal-to-Trial Prioritization

Not all observational signals warrant pragmatic trial confirmation. We propose a Trial Priority Score (TPS) combining:

\[TPS = PIS \times \sqrt{DALYs_{addressable}} \times \text{Novelty} \times \text{Feasibility}\]

Where:

PIS: Predictor Impact Score from Stage 1 (higher = stronger signal)
DALYs_{addressable}: Disease burden addressable by the treatment
Novelty: Inverse of existing evidence (new signals prioritized)
Feasibility: Practical considerations (drug availability, safety profile, cost)

Signals in the top 0.1-1% by TPS are candidates for pragmatic trial confirmation.

14.4 Comparative Effectiveness Randomization

For treatments already in clinical use, we employ comparative effectiveness designs following the ADAPTABLE trial model¹¹:

Embedded randomization: Randomization occurs within routine care visits
Minimal disruption: Patients receive standard care with random assignment between active comparators
Real-world endpoints: Primary outcomes are events captured in EHR (mortality, hospitalization, symptom resolution)
Large simple design: Thousands of patients, minimal per-patient data collection

Example protocol for a high-PIS signal (Treatment A vs. Treatment B for Outcome X):

Table 8: Example pragmatic trial protocol for comparative effectiveness.

Parameter	Specification
Eligibility	Patients with Condition Y initiating treatment for Outcome X
Randomization	1:1 to Treatment A vs. Treatment B
Primary endpoint	Change in Outcome X at 90 days
Data collection	Baseline characteristics (EHR), outcome at 90 days (patient-reported or EHR)
Sample size	2,000 patients (1,000 per arm)
Cost	~$1M total ($500 (95% CI: $400-$2.50K)/patient)
Timeline	6-12 months

14.5 Feedback Loop: Trial Results Improve Observational Models

Pragmatic trial results feed back to improve Stage 1 methodology:

Calibration: Compare observational effect sizes to randomized effect sizes; develop correction factors
Confounding identification: Trials where observational and randomized effects diverge identify confounders
Subgroup discovery: Trial heterogeneity analysis identifies responder populations, improving PIS stratification
Hyperparameter validation: Optimal onset delays and durations validated against experimental ground truth

This creates a learning health system where observational and experimental evidence continuously refine each other.

14.6 Output: Validated Outcome Labels

The two-stage pipeline produces validated outcome labels combining observational and experimental evidence. Table 9 shows the data elements captured for each treatment-outcome pair.

Table 9: Validated outcome label data structure.

Component	Field	Description	Example
Identification	Treatment	Intervention name and dose	Vitamin D 2000 IU
	Outcome	Health outcome measured	Depression Severity
Stage 1 (Observational)	$\Delta_{obs}$	Observational effect size	−12%
	$\text{CI}_{obs}$	95% confidence interval	[−15%, −9%]
	$N_{obs}$	Number of participants	45,000
	PIS	Predictor Impact Score	0.72
Stage 2 (Experimental)	$\Delta_{exp}$	Randomized trial effect	−8%
	$\text{CI}_{exp}$	Trial confidence interval	[−12%, −4%]
	$N_{exp}$	Trial participants	3,000
	Trial ID	Registry identifier	DFDA-VIT-D-001
Combined	Evidence Grade	Validation status	Validated/Promising/Signal
	Causal Confidence	Probability of true effect	0-1 scale

Evidence grades:

Validated: Confirmed by pragmatic RCT (p < 0.05, consistent direction)
Promising: High PIS (>0.6), awaiting or in trial
Signal: Moderate PIS (0.3-0.6), hypothesis only

15 Limitations and How They’re Addressed

The two-stage design addresses the fundamental limitations of purely observational pharmacovigilance while acknowledging residual constraints.

15.1 Fundamental Limitations: Observational Stage

These limitations apply to Stage 1 (observational analysis) but are addressed by Stage 2 (pragmatic trials):

Limitation	Stage 1 Status	Stage 2 Resolution
Cannot prove causation	Hypothesis only	Randomization establishes causation
Cannot replace RCTs	Generates candidates	Pragmatic trials ARE simplified RCTs
Cannot handle strong confounding	Confounding by indication	Randomization eliminates confounding
Cannot generalize beyond population	Self-selected trackers	Pragmatic trials use real-world populations

15.2 Methodological Weaknesses: Addressed by Two-Stage Design

Weakness	Stage 1 Impact	Two-Stage Resolution
Arbitrary baseline definition	Acceptable for signal ranking	Trial uses randomized comparison, no baseline needed
Hyperparameter overfitting	May inflate some correlations	Trial confirms true effect, calibrates models
Self-selection bias	Non-representative sample	Pragmatic trials embed in routine care
Measurement error	Self-report limitations	Trials can use objective endpoints
Hawthorne effect	Tracking changes behavior	Trials embedded in normal care minimize this
Multiple testing	Millions of comparisons	Only top signals proceed to trial (TPS filter)
Temporal confounding	Seasonal/life event effects	Randomization eliminates systematic bias
Confounding by indication	Sicker patients take more treatment	Randomization balances severity

15.3 Residual Limitations

Even with the two-stage design, certain limitations remain:

Resource constraints: Cannot trial all promising signals; prioritization required
External validity: Pragmatic trial populations still may not represent all subgroups
Rare outcomes: Very rare adverse events may require larger observational signals
Behavioral interventions: Some treatments (diet, exercise) difficult to blind
Long-term effects: Pragmatic trials typically 6-12 months; decades-long effects require observational follow-up
Interaction effects: Two-way drug interactions testable; higher-order interactions remain observational

15.4 What This Framework CAN Now Do

With pragmatic trial integration, the complete framework can:

Establish causation: For high-priority signals, randomization proves causal relationships
Generate validated outcome labels: Quantitative effect sizes with experimental backing
Scale discovery: Analyze millions of pairs observationally, confirm thousands experimentally
Continuous validation: Learning loop improves both observational and experimental components
Enable precision medicine: Subgroup analyses identify responders vs. non-responders
Inform regulatory decisions: Validated labels provide evidence for treatment recommendations
Reduce research waste: Focus expensive trials on signals most likely to confirm

16 Implementation Guide

16.1 System Architecture

The framework consists of five sequential processing layers:

Data Ingestion Layer: Collects measurements from wearables, health apps, EHR/FHIR systems, manual entry, and environmental sensors
Measurement Normalization: Standardizes units, timestamps, deduplicates records, and attributes data provenance
Variable Ontology: Assigns semantic categories, default temporal parameters ($\delta$, $\tau$), and filling value logic
Relationship Analysis Engine: Generates predictor-outcome pairs, performs temporal alignment, computes correlations, and optimizes hyperparameters
Population Aggregation: Combines individual N-of-1 analyses, computes confidence intervals, detects heterogeneity and subgroups
Report Generation: Produces outcome labels, treatment rankings, and safety/efficacy signals

Complete implementation details, database schemas, and reference code are available in the supplementary materials repository.

16.2 Core Algorithm: Pair Generation

Algorithm 1 (Temporal Pair Generation): Given predictor measurements $P = \{(t_j^P, p_j)\}$ and outcome measurements $O = \{(t_k^O, o_k)\}$, onset delay $\delta$, duration of action $\tau$, and optional filling value $f$:

Case 1 (Predictor has filling value): For each outcome measurement $(t_k^O, o_k)$: \[p_k = \begin{cases} \frac{1}{|W_k|}\sum_{j \in W_k} p_j & \text{if } W_k \neq \emptyset \\ f & \text{otherwise} \end{cases}\] where $W_k = \{j : t_k^O - \delta - \tau < t_j^P \leq t_k^O - \delta\}$. Output pair $(p_k, o_k)$.

Case 2 (No filling value): For each predictor measurement $(t_j^P, p_j)$: \[o_j = \frac{1}{|W_j|}\sum_{k \in W_j} o_k\] where $W_j = \{k : t_j^P + \delta \leq t_k^O < t_j^P + \delta + \tau\}$. Output pair $(p_j, o_j)$ only if $W_j \neq \emptyset$.

16.3 Core Algorithm: Baseline Separation

Algorithm 2 (Baseline/Follow-up Partition): Given aligned pairs $\{(p_i, o_i)\}_{i=1}^n$:

Compute predictor mean: $\bar{p} = \frac{1}{n}\sum_{i=1}^n p_i$
Partition into baseline $B = \{(p_i, o_i) : p_i < \bar{p}\}$ and follow-up $F = \{(p_i, o_i) : p_i \geq \bar{p}\}$
Compute outcome means: $\mu_B = \mathbb{E}[o \mid (p,o) \in B]$ and $\mu_F = \mathbb{E}[o \mid (p,o) \in F]$
Return percent change: $\Delta = \frac{\mu_F - \mu_B}{\mu_B} \times 100$

16.4 Core Algorithm: Predictor Impact Score

def calculate_user_pis(correlation, statistical_significance, z_score,
                        interest_factor, aggregate_pis):
    """
    Calculate user-level PIS for individual N-of-1 analysis.

    PIS_user = |r| × S × φ_z × φ_temporal × f_interest + PIS_agg
    """
    Z_REF = 2  # Reference z-score (significance threshold)

    # Strength: absolute correlation
    r = abs(correlation.forward_pearson)

    # Effect magnitude: normalized z-score factor
    phi_z = abs(z_score) / (abs(z_score) + Z_REF) if z_score else 0.5

    # Temporality: forward vs reverse correlation ratio
    r_fwd = abs(correlation.forward_pearson)
    r_rev = abs(correlation.reverse_pearson)
    phi_temporal = r_fwd / (r_fwd + r_rev) if (r_fwd + r_rev) > 0 else 0.5

    # Composite user-level score
    radar = r * statistical_significance * phi_z * phi_temporal * interest_factor
    radar += aggregate_pis

    return round(radar, 4)


def calculate_aggregate_pis(correlation, n_users, n_pairs,
                             high_outcome_change, low_outcome_change,
                             weighted_avg_vote, gradient_coefficient):
    """
    Calculate population-level aggregate PIS.

    PIS_agg = |r_forward| × w × φ_users × φ_pairs × φ_change × φ_gradient
    """
    SIGNIFICANT_USERS = 10
    SIGNIFICANT_PAIRS = 100
    SIGNIFICANT_CHANGE_SPREAD = 10

    # Strength: absolute forward correlation
    r_forward = abs(correlation.forward_pearson)

    # Consistency: user saturation
    user_saturation = 1 - exp(-n_users / SIGNIFICANT_USERS)

    # Consistency: pair saturation
    pair_saturation = 1 - exp(-n_pairs / SIGNIFICANT_PAIRS)

    # Clinical significance: change spread saturation
    change_spread = abs(high_outcome_change - low_outcome_change)
    if change_spread == 0:
        change_spread = 1  # Prevent zero PIS
    change_saturation = 1 - exp(-change_spread / SIGNIFICANT_CHANGE_SPREAD)

    # Biological gradient: dose-response
    gradient_factor = min(gradient_coefficient, 1.0)  # Cap at 1.0

    # Composite aggregate score
    radar = (r_forward * weighted_avg_vote * user_saturation *
            pair_saturation * change_saturation * gradient_factor)

    return round(radar, 4)


def calculate_z_score(outcome_percent_change, baseline_rsd):
    """
    Calculate z-score: effect magnitude normalized by baseline variability.

    z = |Δ%| / RSD_baseline

    z > 2 indicates p < 0.05 (statistically significant)
    """
    if baseline_rsd and baseline_rsd > 0:
        return round(abs(outcome_percent_change) / baseline_rsd, 2)
    return None


def calculate_temporality_factor(forward_correlation, reverse_correlation):
    """
    Calculate temporality factor: evidence for forward causation.

    φ_temporal = |r_forward| / (|r_forward| + |r_reverse|)

    Returns 0.5 if ambiguous, approaches 1 if forward dominates.
    """
    r_fwd = abs(forward_correlation)
    r_rev = abs(reverse_correlation)
    if r_fwd + r_rev == 0:
        return 0.5  # No evidence either way
    return round(r_fwd / (r_fwd + r_rev), 4)


def calculate_percent_change_from_baseline(baseline_mean, followup_mean,
                                            is_percent_unit=False):
    """
    Calculate percent change from baseline.

    Δ% = ((followup - baseline) / baseline) × 100
    """
    if baseline_mean == 0 or is_percent_unit:
        return round(followup_mean - baseline_mean, 1)
    return round((followup_mean - baseline_mean) / baseline_mean * 100, 1)


def calculate_interest_factor(predictor_var, outcome_var):
    """
    Calculate interest factor penalizing spurious variable pairs.

    f_interest = f_predictor × f_outcome × f_pair
    """
    factor = 1.0

    # Predictor-specific penalties
    if predictor_var.is_test_variable():
        factor /= 2
    if predictor_var.is_app_or_website():
        factor /= 2
    if predictor_var.is_address():
        factor /= 2

    # Outcome-specific penalties
    if outcome_var.is_test_variable():
        factor /= 2
    if not outcome_var.is_outcome():
        factor /= 2

    # Pair appropriateness
    if not predictor_var.is_predictor():
        factor /= 2
    if is_illogical_category_pair(predictor_var, outcome_var):
        factor /= 10

    return factor

16.5 Database Schema (Key Tables)

-- Variables (predictors, outcomes, etc.)
CREATE TABLE variables (
    id INT PRIMARY KEY,
    name VARCHAR(255),
    variable_category_id INT,
    default_unit_id INT,
    filling_value FLOAT,
    filling_type ENUM('zero', 'value', 'none', 'interpolation'),
    onset_delay INT,  -- seconds, default delay before effect
    duration_of_action INT,  -- seconds, how long effect persists
    outcome BOOLEAN,  -- is this an outcome variable?
    predictor_only BOOLEAN,  -- can only be a predictor (e.g., weather)
    valence ENUM('positive', 'negative', 'neutral'),  -- interpretation of higher values
    is_goal BOOLEAN,  -- something users want to optimize
    controllable BOOLEAN,  -- user can directly modify
    boring BOOLEAN,  -- filter flag for uninteresting variables
    predictor BOOLEAN,  -- can influence outcomes
    optimal_value_message VARCHAR(500),  -- pre-computed recommendation text
    best_predictor_variable_id INT,  -- strongest predictor for this outcome
    best_outcome_variable_id INT  -- most affected outcome by this predictor
);

-- Measurements
CREATE TABLE measurements (
    id BIGINT PRIMARY KEY,
    user_id BIGINT,
    variable_id INT,
    value FLOAT,
    unit_id INT,
    start_time TIMESTAMP,
    source_id INT
);

-- Individual variable relationships (per-user N-of-1 analyses)
-- Contains correlation coefficients, effect sizes, PIS scores, and Bradford Hill metrics
CREATE TABLE user_variable_relationships (
    id BIGINT PRIMARY KEY,
    user_id BIGINT,
    predictor_variable_id INT,
    outcome_variable_id INT,

    -- Correlation coefficients
    forward_pearson_correlation_coefficient FLOAT,  -- Pearson r
    reverse_pearson_correlation_coefficient FLOAT,  -- reverse r (for temporality)
    forward_spearman_correlation_coefficient FLOAT,  -- Spearman r (robust)
    predictive_pearson_correlation_coefficient FLOAT,  -- with optimized params

    -- Temporal parameters
    onset_delay INT,  -- optimized delay (seconds)
    duration_of_action INT,  -- optimized duration (seconds)
    onset_delay_with_strongest_pearson_correlation INT,  -- best delay found
    correlations_over_delays TEXT,  -- JSON: r values for each tested delay
    correlations_over_durations TEXT,  -- JSON: r values for each tested duration

    -- Effect size metrics
    outcome_follow_up_percent_change_from_baseline FLOAT,  -- Δ%
    average_outcome FLOAT,  -- mean outcome
    average_outcome_following_high_predictor FLOAT,  -- outcome when predictor > mean
    average_outcome_following_low_predictor FLOAT,  -- outcome when predictor < mean
    average_daily_high_predictor FLOAT,  -- high predictor value
    average_daily_low_predictor FLOAT,  -- low predictor value
    predicts_high_outcome_change INT,  -- % change at high predictor
    predicts_low_outcome_change INT,  -- % change at low predictor

    -- Baseline/treatment metrics
    outcome_baseline_average FLOAT,
    outcome_baseline_standard_deviation FLOAT,
    outcome_baseline_relative_standard_deviation FLOAT,  -- RSD
    outcome_follow_up_average FLOAT,
    predictor_baseline_average_per_day FLOAT,  -- non-treatment daily avg
    predictor_treatment_average_per_day FLOAT,  -- treatment daily avg
    predictor_baseline_average_per_duration_of_action FLOAT,
    predictor_treatment_average_per_duration_of_action FLOAT,

    -- Statistical significance
    z_score FLOAT,  -- effect magnitude / baseline RSD
    p_value FLOAT,
    t_value FLOAT,
    critical_t_value FLOAT,
    confidence_interval FLOAT,
    statistical_significance FLOAT,

    -- Optimal values for precision dosing
    value_predicting_high_outcome FLOAT,  -- V_high
    value_predicting_low_outcome FLOAT,  -- V_low
    grouped_predictor_value_closest_to_value_predicting_high_outcome FLOAT,
    grouped_predictor_value_closest_to_value_predicting_low_outcome FLOAT,

    -- Quality metrics
    predicted_impact_score FLOAT,  -- PIS_user
    number_of_pairs INT,
    predictor_changes INT,  -- variance in predictor
    outcome_changes INT,  -- variance in outcome

    -- Relationship classification
    strength_level ENUM('VERY STRONG', 'STRONG', 'MODERATE', 'WEAK', 'VERY WEAK'),
    confidence_level ENUM('HIGH', 'MEDIUM', 'LOW'),
    relationship ENUM('POSITIVE', 'NEGATIVE', 'NONE'),

    -- Quality filters
    boring BOOLEAN,
    outcome_is_goal BOOLEAN,
    predictor_is_controllable BOOLEAN,
    plausibly_causal BOOLEAN,
    obvious BOOLEAN,
    interesting_variable_category_pair BOOLEAN,

    -- User feedback
    usefulness_vote INT,  -- -1, 0, 1
    causality_vote INT,  -- -1, 0, 1
    number_of_up_votes INT,
    number_of_down_votes INT
);

-- Population-level variable relationships (aggregated N-of-1 analyses)
-- Combines individual analyses across participants for population-level estimates
CREATE TABLE global_variable_relationships (
    id BIGINT PRIMARY KEY,
    predictor_variable_id INT,
    outcome_variable_id INT,

    -- Aggregated correlation coefficients
    forward_pearson_correlation_coefficient FLOAT,
    reverse_pearson_correlation_coefficient FLOAT,
    predictive_pearson_correlation_coefficient FLOAT,
    population_trait_pearson_correlation_coefficient FLOAT,  -- user-level avg correlation

    -- Sample size metrics
    number_of_users INT,  -- N participants
    number_of_correlations INT,  -- individual analyses aggregated
    number_of_pairs INT,  -- total pairs across all users

    -- Aggregated effect sizes
    outcome_follow_up_percent_change_from_baseline FLOAT,
    aggregate_predicted_impact_score FLOAT,  -- PIS_agg
    gradient_coefficient FLOAT,  -- φ_gradient: dose-response
    confidence_level ENUM('high', 'medium', 'low'),
    up_votes INT,
    down_votes INT,
    -- Population-level optimal values for precision dosing
    average_daily_high_predictor FLOAT,       -- Avg predictor in upper 51% of spread
    average_daily_low_predictor FLOAT,        -- Avg predictor in lower 49% of spread
    value_predicting_high_outcome FLOAT,  -- Population avg V_high
    value_predicting_low_outcome FLOAT    -- Population avg V_low
);

17 Regulatory Considerations

17.1 Positioning Relative to RCTs

This framework is not intended to:

Replace RCTs for regulatory approval
Provide definitive causal proof
Serve as sole basis for clinical decisions

This framework is intended to:

Complement spontaneous reporting with quantitative signals
Prioritize hypotheses for experimental investigation
Provide continuous post-market surveillance
Enable real-time safety signal detection
Generate evidence for benefit-risk reassessment

17.2 Evidence Hierarchy Integration

Evidence Level	Source	Role of This Framework
Level I	RCTs, Meta-analyses	Gold standard for approval
Level II	Cohort studies	This framework provides quantitative RWE
Level III	Case-control	Traditional pharmacovigilance
Level IV	Case series	Spontaneous reports (FAERS)

17.3 FDA Real-World Evidence Framework Alignment

The 21st Century Cures Act mandates FDA evaluation of RWE. This framework supports:

FDA Sentinel System: Provides complementary patient-reported data
Post-market commitments: Continuous safety monitoring
Label updates: Quantitative basis for efficacy/safety updates
Comparative effectiveness: Treatment rankings within classes

18 Validation Framework

18.1 The Critical Question

The ultimate test of PIS validity: Do high-PIS relationships replicate in RCTs more often than low-PIS ones?

Until this validation is performed, PIS should be treated as a theoretically-motivated heuristic, not a validated predictive tool.

18.2 Proposed Validation Study

Design: Retrospective comparison of PIS predictions against published RCT results.

Method: 1. Identify treatment-outcome pairs where both (a) we have sufficient observational data to compute PIS, and (b) RCT evidence exists 2. Compute PIS for each pair using only data collected before RCT publication 3. Compare PIS rankings to RCT effect sizes 4. Assess calibration: Do high-PIS pairs show larger RCT effects?

Success Metrics:

Discrimination: AUC for PIS predicting “RCT shows significant effect” (yes/no)
Calibration: Correlation between PIS and RCT effect size
Prioritization value: Proportion of high-PIS pairs validated by RCT vs. low-PIS pairs

Expected Outcomes:

If PIS ≥ 0.5 pairs have RCT validation rate of 60%+ and PIS < 0.1 pairs have rate < 20%, the metric has practical utility
If no discrimination, saturation constants need recalibration or the approach needs fundamental revision

18.3 Known Limitations Requiring Validation

Confounding by indication: Does the temporality factor adequately address reverse causation in treatment contexts?
Saturation constant sensitivity: How robust are rankings to ±50% changes in N_sig, n_sig?
Population generalizability: Do PIS values from health-tracker users predict effects in general populations?

19 Future Directions

19.1 Methodological Improvements

Causal discovery algorithms: Implement PC algorithm, FCI, or GES for graph structure learning
Propensity score integration: Covariate adjustment for measured confounders
Bayesian hierarchical models: More principled cross-participant pooling with uncertainty quantification
Time-varying effects: Model how relationships change over time (effect modification)
Subgroup analysis: Identify responder vs. non-responder populations using heterogeneity metrics
Multiple testing correction: Benjamini-Hochberg for family-wise error control across millions of pairs
Sensitivity analysis: E-values or other methods to quantify robustness to unmeasured confounding
Causal mediation: Identify mechanisms through which treatments affect outcomes
Drug-drug interactions: Detect combination effects and synergies

19.2 Validation Priorities

Retrospective RCT comparison: Compare PIS predictions to published trial results (highest priority)
Prospective prediction study: Pre-register PIS predictions, validate against future RCTs
Domain expert review: Have clinicians and pharmacologists assess biological plausibility of top PIS relationships
Sensitivity benchmarking: Test robustness to different saturation constants and aggregation methods

19.3 Implementation Enhancements

Real-time signal detection: Automated alerts when new high-PIS relationships emerge
Confidence intervals for PIS: Bootstrap or Bayesian intervals to quantify uncertainty
Interactive exploration: Tools for users to explore their individual PIS relationships
API access: Enable researchers to query PIS data programmatically

20 Conclusion

We have presented a comprehensive two-stage framework for generating validated outcome labels from real-world health data. Key contributions include:

Stage 1: Scalable signal detection: Aggregated N-of-1 observational analysis processes millions of treatment-outcome pairs at ~$0.10/patient, generating ranked hypotheses through the Predictor Impact Score
Stage 2: Causal confirmation: Pragmatic randomized trials following the RECOVERY/ADAPTABLE model confirm top signals at ~$500 (95% CI: $400-$2.50K)/patient (82x (95% CI: 50x-94.1x) cheaper than traditional trials) while eliminating confounding
Bradford Hill operationalization: Six of nine causality criteria quantified in composite scoring system
Trial Priority Score: Principled prioritization of which signals warrant experimental confirmation
Validated outcome labels: Three-tier evidence grading (Validated, Promising, Signal) with both observational and experimental effect sizes
Learning health system: Feedback loop where trial results continuously calibrate observational models

This two-stage design directly addresses the fundamental limitations of purely observational pharmacovigilance. Confounding by indication, self-selection bias, and inability to prove causation are all resolved through Stage 2 randomization for high-priority signals, while Stage 1 maintains the scale and cost advantages necessary for comprehensive monitoring.

This framework represents the FDA of the Future, a decentralized system that:

Receives continuous real-world evidence streams from millions of participants
Generates ranked treatment-outcome hypotheses through automated observational analysis
Confirms top signals through embedded pragmatic trials at 82x (95% CI: 50x-94.1x) lower cost than traditional methods
Publishes validated outcome labels with quantitative effect sizes and evidence grades
Maintains treatment rankings updated in real-time with experimental backing
Enables precision medicine through personalized optimal value calculations
Operates transparently with open-source methodology and reproducible analyses

The technology exists. The methodology is sound. The data is available. The pragmatic trial model is proven. We present this framework not as a replacement for regulatory bodies, but as the complete infrastructure (from passive data collection to validated causal claims) that they will need to fulfill their mission in an era of ubiquitous health data. What remains is the institutional will to build it.

21 Appendix A: Effect Size Classification

Absolute Correlation	Classification
$\\|r\\| \geq 0.8$	Very Strong
$0.6 \leq \\|r\\| < 0.8$	Strong
$0.4 \leq \\|r\\| < 0.6$	Moderate
$0.2 \leq \\|r\\| < 0.4$	Weak
$\\|r\\| < 0.2$	Very Weak

22 Appendix B: Variable Category Defaults

Category	Onset Delay	Duration of Action	Filling Value
Treatments	1,800s (30 min)	86,400s (1 day)	0
Foods	1,800s (30 min)	864,000s (10 days)	0
Emotions	0	86,400s (1 day)	None
Symptoms	0	86,400s (1 day)	None
Vital Signs	0	86,400s (1 day)	None
Sleep	0	86,400s (1 day)	None
Physical Activity	0	86,400s (1 day)	None
Environment	0	86,400s (1 day)	None

23 Appendix C: Glossary

Predictor Variable: The independent variable hypothesized to influence the outcome (e.g., treatment, food, activity). Formerly called “cause variable.”
Outcome Variable: The dependent variable being measured for changes (e.g., symptom, mood, biomarker). Formerly called “effect variable.”
User Variable Relationship: A per-user N-of-1 analysis record containing correlation coefficients, effect sizes (percent change from baseline), Predictor Impact Scores, and Bradford Hill metrics for a specific predictor-outcome pair. Stored in user_variable_relationships table.
Global Variable Relationship: A population-level aggregation of user variable relationships, combining individual N-of-1 analyses across participants. Stored in global_variable_relationships table.
Correlation Coefficient: The Pearson or Spearman statistical measure of linear/monotonic association between predictor and outcome variables (a component of a variable relationship).
Predictor Impact Score (PIS): Composite metric quantifying how much a predictor impacts an outcome. Integrates correlation strength, statistical significance, z-score (effect magnitude), temporality factor, and interest factor at the user level; adds consistency, plausibility, and biological gradient at the aggregate level. Higher scores indicate predictors with greater, more reliable impact. Ranges from 0 to ~1.
Onset Delay ($\delta$): Time between predictor exposure and first observable outcome change
Duration of Action ($\tau$): Time window over which predictor influence on outcome persists
Baseline Period: Measurements when predictor exposure is below participant’s average
Follow-up Period: Measurements when predictor exposure is at or above participant’s average
Percent Change from Baseline ($\Delta\%$): Relative difference between follow-up and baseline outcome means
Z-Score: Effect magnitude normalized by baseline variability; z > 2 indicates statistical significance
Temporality Factor ($\phi_{\text{temporal}}$): Ratio of forward to total correlation, measuring evidence for correct causal direction
Filling Value: Default value imputed for missing measurements
Outcome Label: A per-outcome document that ranks all treatments and predictors by their quantitative effect size on a specific health outcome. Unlike traditional FDA drug labels (which are per-drug and qualitative), outcome labels are per-outcome, quantitative, and dynamically updated. They answer the question: “What works best for this condition?” See Section 7.5 for comparison with FDA labels.
Treatment Ranking: Ordered list of treatments by efficacy or safety for a given outcome, sorted by effect size with confidence weighting. Rankings include percent change from baseline, confidence intervals, sample sizes, and Predictor Impact Scores. See Section 8 for ranking methodology.
Value Predicting High Outcome ($V_{\text{high}}$): The average predictor value observed when the outcome exceeds its mean. Used for precision dosing recommendations. This is the “optimal daily value” for achieving better outcomes.
Value Predicting Low Outcome ($V_{\text{low}}$): The average predictor value observed when the outcome is below its mean. Represents the predictor value associated with worse outcomes.
Grouped Optimal Value: The nearest commonly-used dosing value to the calculated optimal value, enabling practical recommendations (e.g., “400mg” instead of “412.7mg”)
Optimal Value Spread ($V_{\text{high}} - V_{\text{low}}$): The difference between high and low outcome predictor values, indicating the magnitude of dose-response effect
Precision Dosing: Personalized treatment recommendations based on an individual’s historical optimal values, enabling targeted interventions at the dose most likely to produce beneficial outcomes
Average Outcome Following High Predictor ($\bar{O}_{\text{high}}$): Mean outcome value observed following above-average predictor exposure
Average Outcome Following Low Predictor ($\bar{O}_{\text{low}}$): Mean outcome value observed following below-average predictor exposure
Predictor Baseline Average: Average predictor value during low-exposure (non-treatment) periods
Predictor Treatment Average: Average predictor value during high-exposure (treatment) periods
Valence: Whether higher values of a variable are inherently good (positive), bad (negative), or context-dependent (neutral)
Predictor Is Controllable: Flag indicating whether the user can directly modify this predictor (e.g., supplements, food, activities)
Outcome Is Goal: Flag indicating whether this outcome is something users want to optimize
Plausibly Causal: Flag indicating whether a plausible biological mechanism exists for this relationship
Boring: Flag indicating relationships unlikely to interest users due to being uncontrollable, non-goal, implausible, or obvious
Interesting Variable Category Pair: Flag for category combinations that are typically meaningful (e.g., Treatment → Symptom)
Usefulness Vote: User rating (-1, 0, 1) on whether knowledge of a relationship is practically useful
Causality Vote: User rating (-1, 0, 1) on whether a plausible causal mechanism exists
Correlations Over Delays: Stored correlation coefficients calculated with various onset delay values for temporal optimization
Correlations Over Durations: Stored correlation coefficients calculated with various duration of action values
Forward Spearman Correlation: Rank-based correlation coefficient that captures monotonic relationships and is robust to outliers
Optimal Value Confidence Interval: Uncertainty bounds around $V_{\text{high}}$ or $V_{\text{low}}$, reflecting reliability of the estimate based on sample size and variance
Optimal Value Stability: Metric measuring how much the optimal value has changed over time; stability < 0.8 indicates significant drift
Adherence Score: Proportion of tracking days where actual predictor value was within ±20% of the recommended optimal value
Dose-Response Detection Threshold: Criterion ($|V_{\text{high}} - V_{\text{low}}| / \sigma_P < 0.5$) below which no meaningful dose-response exists
Rolling Window Optimal Value: Optimal value calculated using only recent data (e.g., 90 days) rather than all historical data, useful when tolerance effects are expected

24 Appendix D: Worked Example

24.1 Example: Calculating Predictor Impact Score for “Magnesium → Sleep Quality”

Given data (hypothetical):

N = 47 users tracked both magnesium supplementation and sleep quality
n = 2,340 paired observations across all users
Forward correlation: r_forward = 0.31
Reverse correlation: r_reverse = 0.12
Percent change from baseline: Δ% = +18.5% (sleep quality improved)
Baseline RSD: 23%
Community votes: 15 up, 2 down
Effect spread: 22% (difference between high and low magnesium outcomes)

Step 1: Calculate z-score

\[z = \frac{|18.5\%|}{23\%} = 0.80\]

Step 2: Calculate temporality factor

\[\phi_{\text{temporal}} = \frac{|0.31|}{|0.31| + |0.12|} = \frac{0.31}{0.43} = 0.72\]

This suggests forward causation (magnesium → sleep) is more likely than reverse (poor sleep → taking magnesium).

Step 3: Calculate saturation factors

User saturation: $\phi_{\text{users}} = 1 - e^{-47/10} = 1 - 0.009 = 0.991$
Pair saturation: $\phi_{\text{pairs}} = 1 - e^{-2340/100} = 1 - e^{-23.4} ≈ 1.0$
Change saturation: $\phi_{\text{change}} = 1 - e^{-22/10} = 1 - 0.11 = 0.89$

Step 4: Calculate plausibility weight

\[w = \frac{15}{15 + 2} = 0.88\]

Step 5: Compute aggregate PIS

\[\text{PIS}_{\text{agg}} = 0.31 × 0.88 × 0.991 × 1.0 × 0.89 × 0.72 = 0.17\]

Interpretation: PIS = 0.17 falls in the “weak evidence” range (0.1-0.3). The relationship shows:

Modest correlation strength (r = 0.31)
Good temporal evidence (φ = 0.72, forward > reverse)
Strong consistency (many users and pairs)
High plausibility (community agrees mechanism is plausible)

Recommendation: This relationship warrants monitoring. As more data accumulates or if effect size increases, it could become a candidate for experimental validation. The temporality factor is encouraging. This doesn’t appear to be reverse causation.

25 Appendix E: Analysis Workflow

Data ingestion: Collect measurements from all sources
Normalization: Standardize units, deduplicate
Variable assignment: Map to ontology, assign category defaults
Pair generation: Create predictor-outcome pairs with temporal alignment
Baseline separation: Partition by below/above average predictor exposure
Correlation calculation: Pearson, Spearman, forward/reverse
Hyperparameter optimization: Find optimal onset delay and duration
Effect size calculation: Percent change from baseline, z-score
Statistical testing: p-value, confidence intervals
Temporality assessment: Forward/reverse correlation ratio
Predictor Impact Score calculation: Composite PIS metric
User variable relationship storage: Save individual N-of-1 analyses
Population aggregation: Combine into global variable relationships
Report generation: Outcome labels, treatment rankings

Decentralized FDA

Corresponding Author: M.P. Sinn, Decentralized FDA Conflicts of Interest: None declared Funding: None Data Availability: Framework is open-source; individual patient data not shared

References

Report, I. Global trial capacity. IQVIA Report: Clinical Trial Subjects Number Drops Due to Decline in COVID-19 Enrollment https://gmdpacademy.org/news/iqvia-report-clinical-trial-subjects-number-drops-due-to-decline-in-covid-19-enrollment/

1.9M participants annually (2022, post-COVID normalization from 4M peak in 2021) Additional sources: https://gmdpacademy.org/news/iqvia-report-clinical-trial-subjects-number-drops-due-to-decline-in-covid-19-enrollment/

(BIO), B. I. O. BIO clinical development success rates 2011-2020. Biotechnology Innovation Organization (BIO) https://go.bio.org/rs/490-EHZ-999/images/ClinicalDevelopmentSuccessRates2011_2020.pdf (2021)

Phase I duration: 2.3 years average Total time to market (Phase I-III + approval): 10.5 years average Phase transition success rates: Phase I→II: 63.2%, Phase II→III: 30.7%, Phase III→Approval: 58.1% Overall probability of approval from Phase I: 12% Note: Largest publicly available study of clinical trial success rates. Efficacy lag = 10.5 - 2.3 = 8.2 years post-safety verification. Additional sources: https://go.bio.org/rs/490-EHZ-999/images/ClinicalDevelopmentSuccessRates2011_2020.pdf

Organization, W. H. WHO global health estimates 2024. World Health Organization https://www.who.int/data/gho/data/themes/mortality-and-global-health-estimates (2024)

Comprehensive mortality and morbidity data by cause, age, sex, country, and year Global mortality: 55-60 million deaths annually Lives saved by modern medicine (vaccines, cardiovascular drugs, oncology): 12M annually (conservative aggregate) Leading causes of death: Cardiovascular disease (17.9M), Cancer (10.3M), Respiratory disease (4.0M) Note: Baseline data for regulatory mortality analysis. Conservative estimate of pharmaceutical impact based on WHO immunization data (4.5M/year from vaccines) + cardiovascular interventions (3.3M/year) + oncology (1.5M/year) + other therapies. Additional sources: https://www.who.int/data/gho/data/themes/mortality-and-global-health-estimates

SofproMed. Phase 3 cost per trial range. SofproMed https://www.sofpromed.com/how-much-does-a-clinical-trial-cost

Phase 3 clinical trials cost between $20 million and $282 million per trial, with significant variation by therapeutic area and trial complexity. Additional sources: https://www.sofpromed.com/how-much-does-a-clinical-trial-cost | https://www.cbo.gov/publication/57126

Oren Cass, M. I. RECOVERY trial cost per patient. Oren Cass https://manhattan.institute/article/slow-costly-clinical-trials-drag-down-biomedical-breakthroughs (2023)

The RECOVERY trial, for example, cost only about
$500 per patient... By contrast, the median per-patient cost of a pivotal trial for a new therapeutic is around \\$41,000. Additional sources: https://manhattan.institute/article/slow-costly-clinical-trials-drag-down-biomedical-breakthroughs

al., N. E. Á. et. RECOVERY trial global lives saved ( 1 million). NHS England: 1 Million Lives Saved https://www.england.nhs.uk/2021/03/covid-treatment-developed-in-the-nhs-saves-a-million-lives/ (2021)

Dexamethasone saved 1 million lives worldwide (NHS England estimate, March 2021, 9 months after discovery). UK alone: 22,000 lives saved. Methodology: Águas et al. Nature Communications 2021 estimated 650,000 lives (range: 240,000-1,400,000) for July-December 2020 alone, based on RECOVERY trial mortality reductions (36% for ventilated, 18% for oxygen-only patients) applied to global COVID hospitalizations. June 2020 announcement: Dexamethasone reduced deaths by up to 1/3 (ventilated patients), 1/5 (oxygen patients). Impact immediate: Adopted into standard care globally within hours of announcement. Additional sources: https://www.england.nhs.uk/2021/03/covid-treatment-developed-in-the-nhs-saves-a-million-lives/ | https://www.nature.com/articles/s41467-021-21134-2 | https://pharmaceutical-journal.com/article/news/steroid-has-saved-the-lives-of-one-million-covid-19-patients-worldwide-figures-show | https://www.recoverytrial.net/news/recovery-trial-celebrates-two-year-anniversary-of-life-saving-dexamethasone-result

NCBI, F. S. via. Trial costs, FDA study. FDA Study via NCBI https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6248200/

Overall, the 138 clinical trials had an estimated median (IQR) cost of
$19.0 million (\\$12.2 million-
$33.1 million)... The clinical trials cost a median (IQR) of \\$41,117 (
$31,802-\\$82,362) per patient. Additional sources: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6248200/

Naihua Duan, C. H. S., Richard L. Kravitz. Single-patient (n-of-1) trials: A pragmatic clinical decision methodology. PubMed https://pubmed.ncbi.nlm.nih.gov/23849149/ (2013)

Single-patient trials (SPTs, a.k.a. n-of-1 trials) are multiple-period crossover trials conducted within individual patients Application of 2,154 single-patient trials in 108 studies for diverse clinical conditions Conditions addressed: neuropsychiatric (36%), musculoskeletal (21%), pulmonary (13%) Published in Journal of Clinical Epidemiology, 66(8 Suppl): S21-S28 DOI: 10.1016/j.jclinepi.2013.04.006 Additional sources: https://pubmed.ncbi.nlm.nih.gov/23849149/ | https://pmc.ncbi.nlm.nih.gov/articles/PMC3972259/ | https://www.sciencedirect.com/science/article/pii/S089543561300156X

Elizabeth O. Lillie, J. D., Bradley Patay. The n-of-1 clinical trial: The ultimate strategy for individualizing medicine? PubMed https://pubmed.ncbi.nlm.nih.gov/21695041/ (2011)

N-of-1 trials consider an individual patient as the sole unit of observation investigating efficacy or side-effects Goal: determine optimal intervention for individual patient using objective data-driven criteria Can leverage randomization, washout, crossover periods, and placebo controls Argues for serious attention given contemporary focus on individualized medicine Published in Personalized Medicine, 8(2): 161-173. DOI: 10.2217/pme.11.7 Additional sources: https://pubmed.ncbi.nlm.nih.gov/21695041/ | https://pmc.ncbi.nlm.nih.gov/articles/PMC3118090/ | https://www.tandfonline.com/doi/full/10.2217/pme.11.7

10.

Professor Martin Landray (co-chief investigator), M. I., quoted in Oren Cass. RECOVERY trial efficiency. Professor Martin Landray (co-chief investigator) https://manhattan.institute/article/slow-costly-clinical-trials-drag-down-biomedical-breakthroughs (2023)

At a cost of $20 million for 48,000 patients, the RECOVERY trial cost about $500 per patient... that is about $50 per patient per answer. Additional sources: https://manhattan.institute/article/slow-costly-clinical-trials-drag-down-biomedical-breakthroughs

11.

Fund, N. C. NIH pragmatic trials: Minimal funding despite 30x cost advantage. NIH Common Fund: HCS Research Collaboratory https://commonfund.nih.gov/hcscollaboratory (2025)

The NIH Pragmatic Trials Collaboratory funds trials at **$500K for planning phase, $1M/year for implementation**—a tiny fraction of NIH’s budget. The ADAPTABLE trial cost **$14 million** for **15,076 patients** (= **$929/patient**) versus **$420 million** for a similar traditional RCT (30x cheaper), yet pragmatic trials remain severely underfunded. PCORnet infrastructure enables real-world trials embedded in healthcare systems, but receives minimal support compared to basic research funding. Additional sources: https://commonfund.nih.gov/hcscollaboratory | https://pcornet.org/wp-content/uploads/2025/08/ADAPTABLE_Lay_Summary_21JUL2025.pdf | https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5604499/

12.

PMC, S. et al. |. FAERS adverse event underreporting rate. PubMed: Empirical estimation of under-reporting in FAERS https://pubmed.ncbi.nlm.nih.gov/28447485/ (2017)

Empirical estimation: Average reporting rate approximately 6%, meaning 94% of adverse events are underreported Variability: 0.01% to 44% for statin events; 0.002% to >100% for biological drugs; 20% to >100% for narrow therapeutic index (NTI) drugs Selective reporting: Serious, unusual events more likely reported than mild or expected ones Newly marketed drugs: Higher reporting rates due to heightened awareness Older drugs: Events often under-reported Note: FAERS voluntary reporting system captures only "tip of the iceberg" of drug safety problems. Under-reporting introduces inherent biases and limitations in pharmacovigilance data Additional sources: https://pubmed.ncbi.nlm.nih.gov/28447485/ | https://pmc.ncbi.nlm.nih.gov/articles/PMC12393772/

13.

IDC, S. /. Wearable device market and adoption statistics. Statista: Wearable Technology https://www.statista.com/topics/1556/wearable-technology/ (2024)

Global wearable device users: 1.1 billion in 2024, projected 1.5 billion by 2028 Smartwatch users: 500 million globally (2024) Fitness tracker users: 300 million globally Primary use cases: Health/fitness tracking (sleep, steps, heart rate, activity) Market value: $186 billion (2024), projected $390 billion by 2030 Additional sources: https://www.statista.com/topics/1556/wearable-technology/ | https://www.idc.com/promo/wearablevendor | https://www.insiderintelligence.com/insights/wearable-technology-healthcare-medical-devices/

14.

Pearl, J. Causality: Models, Reasoning, and Inference. (Pearl, 2009).

Foundational text on causal inference introducing do-calculus, structural causal models (SCMs), and graphical causal models Provides mathematical framework for defining and computing causal effects from observational and experimental data Introduces key concepts: interventions (do operator), confounding, counterfactuals, d-separation, causal discovery algorithms First edition 2000, second edition 2009 with new material on counterfactuals and mediation Over 45,000 citations - the seminal work that launched modern causal inference as a discipline Additional sources: https://www.cambridge.org/core/books/causality/B0046844FAE10CBF274D4ACBDAEB5F5B | https://www.amazon.com/Causality-Reasoning-Inference-Judea-Pearl/dp/052189560X | https://scholar.google.com/citations?view_op=view_citation&citation_for_view=bAipNH8AAAAJ:8k81kl-MbHgC

15.

Miguel A. Hernán, J. M. R. Causal Inference: What If. (Official Book Website, 2024).

Freely available online textbook on causal inference for scientists who design studies and analyze data Covers counterfactuals, DAGs, randomized experiments, confounding, selection bias, inverse probability weighting, g-estimation, instrumental variables Publisher: Chapman & Hall/CRC Continuously updated - current version available at author’s website Additional sources: https://www.hsph.harvard.edu/miguel-hernan/causal-inference-book/ | https://content.sph.harvard.edu/wwwhsph/sites/1268/2024/01/hernanrobins_WhatIf_2jan24.pdf | https://remlapmot.github.io/cibookex-r/

16.

Hill, A. B. The environment and disease: Association or causation? PubMed Central: Hill 1965 https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1898525/ (1965)

Original paper establishing the 9 criteria for evaluating causal relationships in epidemiology Criteria: Strength, Consistency, Specificity, Temporality, Biological Gradient, Plausibility, Coherence, Experiment, Analogy Published in Proceedings of the Royal Society of Medicine Most influential framework for assessing causation from observational data Additional sources: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1898525/ | https://en.wikipedia.org/wiki/Bradford_Hill_criteria

Footnotes

St. John’s Wort shows high heterogeneity (some responders, some non-responders)↩︎

Reuse

CC BY-NC 4.0